题目内容
16.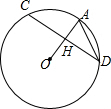 如图,OA是⊙O的半径,弦CD⊥OA,垂足为H,连接AD.
如图,OA是⊙O的半径,弦CD⊥OA,垂足为H,连接AD.(1)若CD=2$\sqrt{2}$,AD=$\sqrt{3}$,求⊙O的半径长;
(2)设OA=r,AD=m,AH=n,求证:m2=2rn.
分析 (1)连接OD,根据垂径定理求出DH,根据勾股定理求出AH,再根据勾股定理列出关于OA的方程,解方程即可;
(2)作直径AG,连接DG,根据射影定理证明.
解答 解:(1) 连接OD,
连接OD,
∵CD⊥OA,
∴DH=$\frac{1}{2}$CD=$\sqrt{2}$,又AD=$\sqrt{3}$,
∴AH=$\sqrt{A{D}^{2}-D{H}^{2}}$=1,
则OH=OA-1,
∴OD2=OH2+DH2,即OA2=(OA-1)2+2,
解得,OA=$\frac{3}{2}$;
(2)证明:作直径AG,连接DG,
∴∠ADG=90°,又CD⊥OA,
∴AD2=AH•AG,
即m2=2rn.
点评 本题考查的是垂径定理、勾股定理和射影定理的综合运用,掌握垂直于弦的直径平分这条弦是解题的关键,解答时注意射影定理成立的条件.

练习册系列答案
相关题目
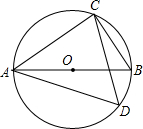 如图,已知AB是⊙O的直径,点CD在⊙O上,且AB=5,BC=3,则sin∠BAC=$\frac{3}{5}$;sin∠ADC=$\frac{4}{5}$.
如图,已知AB是⊙O的直径,点CD在⊙O上,且AB=5,BC=3,则sin∠BAC=$\frac{3}{5}$;sin∠ADC=$\frac{4}{5}$.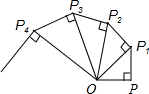 如图,OP=1,过P作PP1⊥OP,且PP1=1;得OP12=OP2+P1P2=12+12=2,再过P1作P1P2⊥OP1且P1P2=1,得OP22=3;又过P2作P2P3⊥OP2且P2P3=1,得OP32=4;…依此方法继续作下去,得OP20122=2013.
如图,OP=1,过P作PP1⊥OP,且PP1=1;得OP12=OP2+P1P2=12+12=2,再过P1作P1P2⊥OP1且P1P2=1,得OP22=3;又过P2作P2P3⊥OP2且P2P3=1,得OP32=4;…依此方法继续作下去,得OP20122=2013. 化简|a+b|+|a-c|-|b|+|b-c|.
化简|a+b|+|a-c|-|b|+|b-c|.