题目内容
17.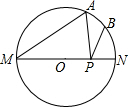 如图,MN是⊙O的直径,MN=4,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为2$\sqrt{3}$.
如图,MN是⊙O的直径,MN=4,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为2$\sqrt{3}$.
分析 过A作关于直线MN的对称点A′,连接A′B,由轴对称的性质可知A′B即为PA+PB的最小值,由对称的性质可知$\widehat{AN}$=$\widehat{A′N}$,再由圆周角定理可求出∠A′ON的度数,再由勾股定理即可求解.
解答  解:过A作关于直线MN的对称点A′,连接A′B,由轴对称的性质可知A′B即为PA+PB的最小值,
解:过A作关于直线MN的对称点A′,连接A′B,由轴对称的性质可知A′B即为PA+PB的最小值,
连接OB,OA′,AA′,
∵AA′关于直线MN对称,
∴$\widehat{AN}$=$\widehat{A′N}$,
∵∠AMN=40°,
∴∠A′ON=80°,∠BON=40°,
∴∠A′OB=120°,
过O作OQ⊥A′B于Q,
在Rt△A′OQ中,OA′=2,
∴A′B=2A′Q=2$\sqrt{3}$,
即PA+PB的最小值2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 本题考查的是轴对称-最短路线问题,圆周角定理及勾股定理,解答此题的关键是根据题意作出辅助线,构造出直角三角形,利用勾股定理求解.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
7.$\root{3}{8}$的算术平方根是( )
| A. | 2 | B. | ±2 | C. | $\sqrt{2}$ | D. | $±\sqrt{2}$ |
9.下列单项式中,与a2b是同类项的是( )
| A. | 2a2b | B. | a2b2 | C. | ab2 | D. | 3ab |
6.下列各曲线中表示y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
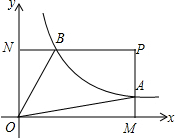 如图,已知点P(6,3),过点P作PM⊥x轴于点M,PN⊥y轴于点N,反比例函数y=$\frac{k}{x}$的图象交PM于点A,交PN于点B.若四边形OAPB的面积为12,则k=6.
如图,已知点P(6,3),过点P作PM⊥x轴于点M,PN⊥y轴于点N,反比例函数y=$\frac{k}{x}$的图象交PM于点A,交PN于点B.若四边形OAPB的面积为12,则k=6. 如图,在△ABC中,AB=BC,∠ABC=110°,AB的垂直平分线DE交AC于点D,连接BD,则∠ABD=35度.
如图,在△ABC中,AB=BC,∠ABC=110°,AB的垂直平分线DE交AC于点D,连接BD,则∠ABD=35度. 如图,由5块完全相同的小正方体所搭成的几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数,其主视图是( )
如图,由5块完全相同的小正方体所搭成的几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数,其主视图是( )



 如图,△ABC沿边BC向右平移2个单位得到△DEF,已知BC=5,则EC=3.
如图,△ABC沿边BC向右平移2个单位得到△DEF,已知BC=5,则EC=3.