题目内容
19.函数y=$\frac{3}{x}$与y=x+1的图象的交点坐标为(a,b),则$\frac{1}{b}-\frac{1}{a}$的值为-$\frac{1}{3}$.分析 把A的坐标代入两函数得出ab=3,b-a=1,把$\frac{1}{b}-\frac{1}{a}$化成$\frac{a-b}{ab}$,代入求出即可.
解答 解:∵函数y=$\frac{3}{x}$与y=x+1的图象的交点坐标为(a,b),
代入得:ab=3,b-a=1,
$\frac{1}{b}-\frac{1}{a}$=$\frac{a-b}{ab}$=-$\frac{1}{3}$,
故答案为:-$\frac{1}{3}$.
点评 本题考查了一次函数与反比例函数的交点问题,解此题的关键是求出ab和b-a的值,题目具有一定的代表性,是一道比较好的题目.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
4.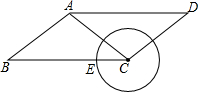 如图,已知平行四边形ABCD中,AB=5,BC=8,cosB=$\frac{4}{5}$,点E是BC边上的动点,当以CE为半径的圆C与边AD不相交时,半径CE的取值范围是( )
如图,已知平行四边形ABCD中,AB=5,BC=8,cosB=$\frac{4}{5}$,点E是BC边上的动点,当以CE为半径的圆C与边AD不相交时,半径CE的取值范围是( )
 如图,已知平行四边形ABCD中,AB=5,BC=8,cosB=$\frac{4}{5}$,点E是BC边上的动点,当以CE为半径的圆C与边AD不相交时,半径CE的取值范围是( )
如图,已知平行四边形ABCD中,AB=5,BC=8,cosB=$\frac{4}{5}$,点E是BC边上的动点,当以CE为半径的圆C与边AD不相交时,半径CE的取值范围是( )| A. | 0<CE≤8 | B. | 0<CE≤5 | C. | 0<CE<3或5<CE≤8 | D. | 3<CE≤5 |
11.(-3)2的结果是( )
| A. | 6 | B. | -6 | C. | 9 | D. | -9 |
 已知在△ABC中,AB=4,AC=3,AB与AC的夹角为α,设△ABC的面积为S.
已知在△ABC中,AB=4,AC=3,AB与AC的夹角为α,设△ABC的面积为S. 4个大小相同的正方体积木摆放成如图所示的几何体,其俯视图是( )
4个大小相同的正方体积木摆放成如图所示的几何体,其俯视图是( )



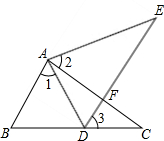 如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE,请找出图中的全等三角形,并给予证明.
如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE,请找出图中的全等三角形,并给予证明.