题目内容
5.在?ABCD中,∠ABC的角平分线BE交边AD所在直线于点E,且AE:ED=2:1,若AD=12cm,则?ABCD的周长是40cm.分析 由?ABCD,根据平行四边形的对边平行且相等,可得AD∥BC,AD=BC,AB=CD,又由BE是∠ABC的平分线,可得∠ABE=∠CBE,易得AE=AB(等角对等边),即可求得?ABCD的周长.
解答 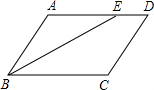 解:如图所示:
解:如图所示:
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,AB=CD,
∴∠AEB=∠CBE,
∵BE是∠ABC的平分线,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∵AE:ED=2:1,AD=12cm,
∴AE=8cm,DE=4cm,
∴AE=AB=8cm,
∴?ABCD的周长=8+8+12+12=40cm.
故答案为:40cm.
点评 本题主要考查了平行四边形的性质,在平行四边形中,当出现角平分线时,一般可构造等腰三角形,进而利用等腰三角形的性质解题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
17.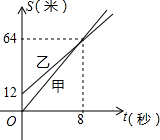 甲、乙两人运动的路程和时间之间的函数关系如图所示,则甲的速度比乙的速度每秒快( )
甲、乙两人运动的路程和时间之间的函数关系如图所示,则甲的速度比乙的速度每秒快( )
 甲、乙两人运动的路程和时间之间的函数关系如图所示,则甲的速度比乙的速度每秒快( )
甲、乙两人运动的路程和时间之间的函数关系如图所示,则甲的速度比乙的速度每秒快( )| A. | 2.5米 | B. | 2米 | C. | 1.5米 | D. | 1米 |
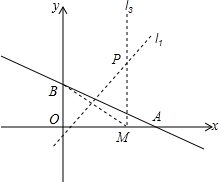 如图:直线y=kx+3与x轴、y轴分别交于A、B两点,tan∠OAB=$\frac{3}{4}$,点M是x轴上的一个动点.连接BM,作线段BN的垂直平分线l1,过点M作x轴垂线l2 记l1与l2的交点为P.
如图:直线y=kx+3与x轴、y轴分别交于A、B两点,tan∠OAB=$\frac{3}{4}$,点M是x轴上的一个动点.连接BM,作线段BN的垂直平分线l1,过点M作x轴垂线l2 记l1与l2的交点为P.