题目内容
7．am=9，an=8，ak=4，则am-2n+3k=9．分析 先根据同底数幂的乘法和除法进行变形，再根据幂的乘方变形，最后代入求出即可．
解答 解：∵am=9，an=8，ak=4，
∴am-2n+3k=am÷a2n•a3k
=am÷（an）2•（ak）3
=9÷82×43
=9，
故答案为：9．
点评 本题考查了同底数幂的乘法和除法，幂的乘方等知识点，能根据法则正确变形是解此题的关键，用了整体代入思想．
练习册系列答案
相关题目
15．下列图形中（如图），∠1和∠2是同位角的有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
2．
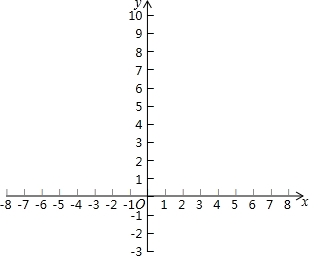有这样一个问题：探究函数$y=\frac{x}{x+1}$的图象与性质．小怀根据学习函数的经验，对函数$y=\frac{x}{x+1}$的图象与性质进行了探究．下面是小怀的探究过程，请补充完成：
（1）函数$y=\frac{x}{x+1}$的自变量x的取值范围是x≠-1；
（2）列出y与x的几组对应值．请直接写出m的值，m=3；
（3）请在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点，并画出该函数的图象；
（4）结合函数的图象，写出函数$y=\frac{x}{x+1}$的一条性质．
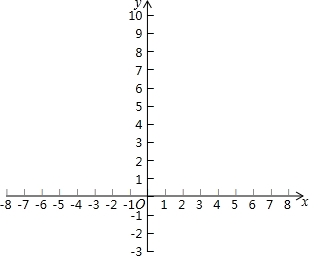有这样一个问题：探究函数$y=\frac{x}{x+1}$的图象与性质．小怀根据学习函数的经验，对函数$y=\frac{x}{x+1}$的图象与性质进行了探究．下面是小怀的探究过程，请补充完成：（1）函数$y=\frac{x}{x+1}$的自变量x的取值范围是x≠-1；
（2）列出y与x的几组对应值．请直接写出m的值，m=3；
（3）请在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点，并画出该函数的图象；
（4）结合函数的图象，写出函数$y=\frac{x}{x+1}$的一条性质．
| x | … | -5 | -4 | -3 | -2 | -$\frac{3}{2}$ | -$\frac{1}{2}$ | 0 | 1 | 2 | m | 4 | 5 | … |
| y | … | $\frac{5}{4}$ | $\frac{4}{3}$ | $\frac{3}{2}$ | 2 | 3 | -1 | 0 | $\frac{1}{2}$ | $\frac{2}{3}$ | $\frac{3}{4}$ | $\frac{4}{5}$ | $\frac{5}{6}$ | … |
19．下列线段中，不可能是同一个三角形的三边上的高的是（ ）
| A． | 1cm，1cm，2cm | B． | 2cm，2cm，1cm | C． | 2cm，3cm，3cm | D． | 3cm，4cm，6cm |
