Question

16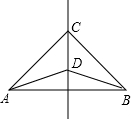．如图，CD是线段AB的垂直平分线，则∠CAD=∠CBD．请说明理由：
解：∵CD是线段AB的垂直平分线，
∴AC=BC，AD=BD．
   在△ACD和△BCD中，

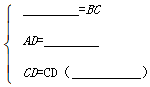
∴△ACD≌△BCD（SSS）．
∴∠CAD=∠CBD．

Answer 1

分析 根据线段垂直平分线性质得出AC=BC，AD=BD，根据SSS证出△ACD≌△BCD即可．

解答 解：∵CD是线段AB的垂直平分线，
∴AC=BC，AD=BD，
在△ACD和△BCD中，$\left\{\begin{array}{l}{AC=BC}\\{AD=BD}\\{CD=CD（公共边）}\end{array}\right.$，
∴△ACD≌△BCD（SSS），
∴∠CAD=∠CBD．
故答案为：BC，AD，AC，BD，公共边，△ACD，△BCD，SSS．

点评 本题考查了全等三角形的性质和判定、线段垂直平分线性质等知识；熟练掌握全等三角形的判定定理是解决问题的关键．