题目内容
观察下列各式是否正确,其中a、b均为非负数.
(1)若a+b=1,则
≤0.5;
(2)若a+b=2,则
≤1;
(3)若a+b=3,则
<1.5;
(4)若a+b=4,则
≤2.
判断完以上各式后,你发现了什么规律?请用含a、b的式子将规律表示出来,并注明a、b的取值范围及等号成立的条件,说明成立的理由.
(1)若a+b=1,则
| ab |
(2)若a+b=2,则
| ab |
(3)若a+b=3,则
| ab |
(4)若a+b=4,则
| ab |
判断完以上各式后,你发现了什么规律?请用含a、b的式子将规律表示出来,并注明a、b的取值范围及等号成立的条件,说明成立的理由.
考点:完全平方公式
专题:规律型
分析:根据观察等式可发现规律:
≥
(a≥0,b≥0).
| a+b |
| 2 |
| ab |
解答:解:其中a、b均为非负数,
(1)若a+b=1,则
≤0.5;
(2)若a+b=2,则
≤1;
(3)若a+b=3,则
<1.5;
(4)若a+b=4,则
≤2.
各式都正确,
规律:
≥
(a≥0,b≥0),理由如下:
(
+
)2=a+b-2
≥0,
a+b≥2
.
(1)若a+b=1,则
| ab |
(2)若a+b=2,则
| ab |
(3)若a+b=3,则
| ab |
(4)若a+b=4,则
| ab |
各式都正确,
规律:
| a+b |
| 2 |
| ab |
(
| a |
| b |
| ab |
a+b≥2
| ab |
点评:本题考查了完全平方公式,利用了和的平方.

练习册系列答案
相关题目
 如图,△ABC的边BC上的高为AD,且BC=9cm,AD=2cm,AC=6cm,求AC边上的高BE的长.
如图,△ABC的边BC上的高为AD,且BC=9cm,AD=2cm,AC=6cm,求AC边上的高BE的长.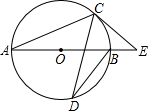 如图所示,线段AB是⊙O上一点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,求∠E的度数.
如图所示,线段AB是⊙O上一点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,求∠E的度数. 如图,在平面直角坐标系中,反比例函数y1=
如图,在平面直角坐标系中,反比例函数y1=