题目内容
已知关于x的方程3(x-2a)=x-a+1的解适合不等式x-3≤4a,求a的取值范围.
考点:解一元一次不等式,一元一次方程的解
专题:
分析:首先求出所给方程的解,然后代入不等式,解不等式即可.
解答:解:∵3(x-2a)=x-a+1,
∴3x-6a=x-a+1,整理得2x=5a+1,
∴x=
;
∵关于x的方程3(x-2a)=x-a+1的解适合不等式x-3≤4a,
∴
-3≤4a,去分母得5a+1-6≤8a,
∴3a≥-5,a≥-
,
∴a的取值范围是a≥-
.
∴3x-6a=x-a+1,整理得2x=5a+1,
∴x=
| 5a+1 |
| 2 |
∵关于x的方程3(x-2a)=x-a+1的解适合不等式x-3≤4a,
∴
| 5a+1 |
| 2 |
∴3a≥-5,a≥-
| 5 |
| 3 |
∴a的取值范围是a≥-
| 5 |
| 3 |
点评:命题考查了一元一次方程、一元一次不等式的解法及其应用问题;解题的关键是准确求出方程的解,将所求解代入不等式,解不等式.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
在方程x2+x=y,
x-2x2=3,(x-1)(x-2)=0,x2-
=4,x(x-1)=1中,一元二次方程的个数是( )
| 5 |
| 1 |
| x |
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,已知在Rt△ABC中,∠ACB=90°,EF是AB的垂直平分线,交AC、AB于点E、F,EF=EC,求∠A的度数.
如图,已知在Rt△ABC中,∠ACB=90°,EF是AB的垂直平分线,交AC、AB于点E、F,EF=EC,求∠A的度数. 如图,Rt△ABC中,∠C=90°,∠B=3∠A,求∠B的度数.
如图,Rt△ABC中,∠C=90°,∠B=3∠A,求∠B的度数.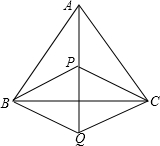 如图,点P是等边△ABC内的一点,连接PA、PB、PC,以BP为一边作∠PBQ=60°,且BQ=BP,连接CQ.
如图,点P是等边△ABC内的一点,连接PA、PB、PC,以BP为一边作∠PBQ=60°,且BQ=BP,连接CQ.