题目内容
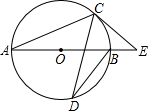如图所示，线段AB是⊙O上一点，∠CDB=20°，过点C作⊙O的切线交AB的延长线于点E，求∠E的度数．考点：切线的性质
专题：
分析：连接OC，根据圆周角的性质得出∠A=∠CDB=20°，进而得出∠COE=40°，根据切线的性质得出∠OCE=90°，根据三角形的内角和即可求得∠E的度数．
解答：
解：连接OC，
∵∠A与∠CDB对
，
∴∠A=∠CDB=20°，
∵OA=OC，
∴∠ACO=∠A=20°，
∴∠COE=40°，
∵CE是⊙O的切线，切点是C，
∴∠OCE=90°，
∴∠E=90°-∠COE=50°
解：连接OC，∵∠A与∠CDB对
 |
| BC |
∴∠A=∠CDB=20°，
∵OA=OC，
∴∠ACO=∠A=20°，
∴∠COE=40°，
∵CE是⊙O的切线，切点是C，
∴∠OCE=90°，
∴∠E=90°-∠COE=50°
点评：本题考查了切线的性质，等腰三角形的性质，三角形的内角和定理，作出辅助线根据直角三角形是关键．
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目
如图，在Rt△ABC中，∠B=90°，AD=AB=BC，DE⊥AC．求证：BE=DC．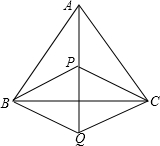
如图，点P是等边△ABC内的一点，连接PA、PB、PC，以BP为一边作∠PBQ=60°，且BQ=BP，连接CQ．
△ABC中，BD平分∠ABC，E为BD上一点，EF⊥AC于F，∠A=40°，∠C=78°，则∠DEF的度数为