题目内容
(1)(a-2b)2(a+2b)2;
(2)(x-y)(x+y)(x2-y2);
(3)(x-y+2z)(x-y-2z).
(2)(x-y)(x+y)(x2-y2);
(3)(x-y+2z)(x-y-2z).
考点:完全平方公式,平方差公式
专题:
分析:(1)逆用积的乘方公式化成【(a-2b)(a+2b)】2,首先利用平方差公式,然后利用完全平方公式计算即可;
(2)利用平方差公式和完全平方公式即可求解;
(3)化成【(x-y)+2z】【(x-y)-2z】的形式,利用平方差公式,然后利用完全平方公式即可求解.
(2)利用平方差公式和完全平方公式即可求解;
(3)化成【(x-y)+2z】【(x-y)-2z】的形式,利用平方差公式,然后利用完全平方公式即可求解.
解答:解:(1)原式=【(a-2b)(a+2b)】2=(a2-4b2)2=a4-8a2b2+16b4;
(2)原式=(x2-y2)2=x4-2x2y2+y4;
(3)原式=【(x-y)+2z】【(x-y)-2z】=(x-y)2-4z2=x2+y2-2xy-4z2.
(2)原式=(x2-y2)2=x4-2x2y2+y4;
(3)原式=【(x-y)+2z】【(x-y)-2z】=(x-y)2-4z2=x2+y2-2xy-4z2.
点评:本题主要考查完全平方公式可平方差公式,注意公式中的a、b可以表示数,也可以表示单项式、也可以表示多项式,熟记公式的几个变形公式对解题大有帮助.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
边长为下列各组数的三角形中,是直角三角形的是( )
A、1、2、
| ||||||
| B、4、5、6 | ||||||
C、
| ||||||
D、2
|
 如图,在B港有甲、乙两艘渔船,若甲船沿北偏东60°方向以每小时8海里速度前进,乙船沿南偏东某方向以每小时15海里速度全速前进,2小时后甲船到M岛,乙船到P岛,两岛相距34海里,你知道乙船沿那个方向航行吗?
如图,在B港有甲、乙两艘渔船,若甲船沿北偏东60°方向以每小时8海里速度前进,乙船沿南偏东某方向以每小时15海里速度全速前进,2小时后甲船到M岛,乙船到P岛,两岛相距34海里,你知道乙船沿那个方向航行吗?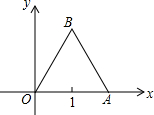 如图,已知等边三角形OAB的一个顶点为A(2,0),求其余两个顶点的坐标.
如图,已知等边三角形OAB的一个顶点为A(2,0),求其余两个顶点的坐标.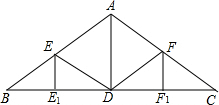 已知:如图的房屋梁架中,AB=AC=4m,∠BAC=120°,点D、E、F分别是BC、AB、AC的中点,且EE1⊥BC,AD⊥BC,FF1⊥BC,求EE1,ED,AD,FD,FF1的长.
已知:如图的房屋梁架中,AB=AC=4m,∠BAC=120°,点D、E、F分别是BC、AB、AC的中点,且EE1⊥BC,AD⊥BC,FF1⊥BC,求EE1,ED,AD,FD,FF1的长.