Question

16．如图，⊙O的半径为6，△ABC是⊙O的内接三角形，连接OB，OC，若∠BAC与∠BOC互补，则弦BC的长是6$\sqrt{3}$．

Answer 1

分析 作弦心距OD，先根据已知求出∠BOC=120°，由等腰三角形三线合一的性质得：∠DOC=$\frac{1}{2}$∠BOC=60°，利用30°角所对的直角边是斜边的一半可求得OD的长，根据勾股定理得DC的长，最后利用垂径定理得出结论．

解答 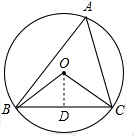解∵∠BAC与∠BOC互补，
∴∠BAC+∠BOC=180°，
∵∠BAC=$\frac{1}{2}$∠BOC，
∴∠BOC=120°，
过O作OD⊥BC，垂足为D，
∴BD=CD，
∵OB=OC，
∴OB平分∠BOC，
∴∠DOC=$\frac{1}{2}$∠BOC=60°，
∴∠OCD=90°-60°=30°，
在Rt△DOC中，OC=6，
∴OD=3，
∴DC=3$\sqrt{3}$，
∴BC=2DC=6$\sqrt{3}$，
故答案为6$\sqrt{3}$．

点评 本题考查三角形的外接圆与外心、锐角三角函数、垂径定理等知识，解题的关键是学会添加常用辅助线，还在直角三角形解决问题，属于中考常考题型．