题目内容
6. 端午节前夕,三位同学到某超市调研一种进价为80元的粽子礼盒的销售情况,请根据小梅提供的信息,解答小慧和小杰提出的问题.(价格取正整数)
端午节前夕,三位同学到某超市调研一种进价为80元的粽子礼盒的销售情况,请根据小梅提供的信息,解答小慧和小杰提出的问题.(价格取正整数)
分析 小慧:设定价为x元,利润为y元,根据利润=(定价-进价)×销售量,列出函数关系式,结合x的取值范围,求出当y取800时,定价x的值即可;
小杰:根据小慧中求出的函数解析式,运用配方法求最大值,并求此时x的值即可.
解答 解:小慧:设定价为x元,利润为y元,则销售量为:410-10(x-100)=1410-10x,
由题意得,y=(x-80)(1410-10x)
=-10x2+2210x-112800,
当y=8580时,-10x2+2210x-112800=8580,
整理,得:x2-221x+12138=0,
解得:x=102或x=119,
∵当x=102时,销量为1410-1020=390,
当x=119时,销量为1410-1190=220,
∴若要达到8580元的利润,且薄利多销,
∴此时的定价应为102元;
小杰:y=-10x2+2210x-112800=-10(x-$\frac{221}{2}$)2+$\frac{18605}{2}$,
∵价格取整数,即x为整数,
∴当x=110或x=111时,y取得最大值,最大值为9300,
答:8580元的销售利润不是最多,当定价为110元或111元时,销售利润最多,最多利润为9300元.
点评 本题考查了二次函数的应用,难度一般,解答本题的关键是根据题意找出等量关系列出函数关系式,要求同学们掌握运用配方法求二次函数的最大值.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
16.李华同学在庆祝元旦歌咏比赛中,6位评委给他的打分如下表,则李华得分众数为90分
| 评委代号 | A | B | C | D | E | F |
| 评分 | 85 | 90 | 80 | 95 | 90 | 90 |
 如图,⊙O的半径为6,△ABC是⊙O的内接三角形,连接OB,OC,若∠BAC与∠BOC互补,则弦BC的长是6$\sqrt{3}$.
如图,⊙O的半径为6,△ABC是⊙O的内接三角形,连接OB,OC,若∠BAC与∠BOC互补,则弦BC的长是6$\sqrt{3}$.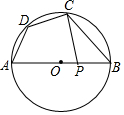 如图,四边形ABCD内接于⊙O,AB为⊙O的直径,∠ADC=130°,点P为半径OB上任意一点,连接CP,则∠BCP可能为30°(写出一个即可)
如图,四边形ABCD内接于⊙O,AB为⊙O的直径,∠ADC=130°,点P为半径OB上任意一点,连接CP,则∠BCP可能为30°(写出一个即可) 在平面直角坐标系xOy中,一次函数y=kx和y=-x+3的图象如图所示,则关于x的一元一次不等式kx<-x+3的解集是x<1.
在平面直角坐标系xOy中,一次函数y=kx和y=-x+3的图象如图所示,则关于x的一元一次不等式kx<-x+3的解集是x<1. 如图是某中学七年级教师年龄(取正整数)的频数分布直方图.根据图形,我们知道,该学校七年级共有教师52人.
如图是某中学七年级教师年龄(取正整数)的频数分布直方图.根据图形,我们知道,该学校七年级共有教师52人.