Question

6．如图，E、F在双曲线y=$\frac{k}{x}$上，EF交y轴于点A，AE=EF，FM⊥x轴于点M，若S_△AME=3，则k=-12．

Answer 1

分析 如图，连接FO，由于S_△AME=3，AE=EF，由此得到△AFM的面积，又FM⊥x轴于M，由此得到FM∥y轴，所以得到△FOM的面积和△AFM的面积相等，由此即可求出k值．

解答 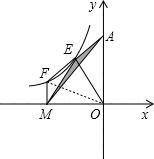解：如图，连接FO，
∵S_△AME=3，AE=EF，
∴S_△AFM=2S_△AME=6，
∵FM⊥x轴于M，
∴FM∥y轴，
∴S_△AFM=S_△OMF=6，即$\frac{1}{2}$×FM×MO=6，FM×MO=12，
又F在双曲线y=$\frac{k}{x}$上，
∴k=-12．
故答案为：-12．

点评 此题主要考查了反比例函数的图象和性质，解题的关键是利用等积变换分别求出相关几个三角形的面积，然后利用面积和反比例函数图象的关系解决问题．