题目内容
(1)电脑公司销售一批计算机,第一个月以5500元/台的价格售出60台,第二个月其降价,以5000元/台的价格将这批计算机全部售出,销售款总额超过55万元,这批计算机最少有多少台?
(2)某校准备组织290名学生进行野外考察活动,行李共有100件.学校计划租用甲、乙两种型号的汽车共8辆.经了解,甲种汽车每辆能载40人和10件,乙种汽车每辆能载30人和20件.
①请你帮助学校设计所有可能的租车方案.
②如果甲、乙两种汽车每辆的租车费用分别为2000元、1800元,请你选择最省钱的一种方案.
(2)某校准备组织290名学生进行野外考察活动,行李共有100件.学校计划租用甲、乙两种型号的汽车共8辆.经了解,甲种汽车每辆能载40人和10件,乙种汽车每辆能载30人和20件.
①请你帮助学校设计所有可能的租车方案.
②如果甲、乙两种汽车每辆的租车费用分别为2000元、1800元,请你选择最省钱的一种方案.
考点:一元一次不等式组的应用,一元一次不等式的应用
专题:
分析:(1)根据题意设这批计算机有x台,第二个月还有(x-60)台,先表示出第一个月销售量,再表示出第二个月销售量,然后用第一个月销售量×单价+第二个月销售量×单价>55万元即可;
(2)①设租用甲种汽车x辆,则租用乙种汽车(8-x)辆,根据总人数是290和行李共有100件,列出出不等式组,求出不等式组的解集,即可得出答案;
②设租车费用为y元,再分别计算甲、乙所需要的费用,然后比较,花费较少的即为最省钱的租车方案.
(2)①设租用甲种汽车x辆,则租用乙种汽车(8-x)辆,根据总人数是290和行李共有100件,列出出不等式组,求出不等式组的解集,即可得出答案;
②设租车费用为y元,再分别计算甲、乙所需要的费用,然后比较,花费较少的即为最省钱的租车方案.
解答:解:(1)设这批计算机最少有x台,根据题意得:
5500×60+5000×(x-60)>550000,
解得:x≥104,
答:这批计算机最少104台;
(2)①设租用甲种汽车x辆,则租用乙种汽车(8-x)辆,由题意得:
,
解得:5≤x≤6,
即共有2种租车方案:
方案一:租用甲种汽车5辆,乙种汽车3辆;
方案二:租用甲种汽车6辆,乙种汽车2辆.
②设租车费用为y元,根据题意得:
y=2000x+1800(8-x)=14400+200x,(5≤x≤6),
∵200>0,
∴y随x增大而增大,
∴当x=5时,取得最小值,y=5×2000+3×1800=15400(元);
∴租用甲种汽车5辆,乙种汽车3辆的方案更省费用.
5500×60+5000×(x-60)>550000,
解得:x≥104,
答:这批计算机最少104台;
(2)①设租用甲种汽车x辆,则租用乙种汽车(8-x)辆,由题意得:
|
解得:5≤x≤6,
即共有2种租车方案:
方案一:租用甲种汽车5辆,乙种汽车3辆;
方案二:租用甲种汽车6辆,乙种汽车2辆.
②设租车费用为y元,根据题意得:
y=2000x+1800(8-x)=14400+200x,(5≤x≤6),
∵200>0,
∴y随x增大而增大,
∴当x=5时,取得最小值,y=5×2000+3×1800=15400(元);
∴租用甲种汽车5辆,乙种汽车3辆的方案更省费用.
点评:此题主要考查了一元一次不等式组的应用,解题的关键是读懂题意,找出题目中的数量关系,列出不等式组.

练习册系列答案
相关题目
 如图,已知∠1=∠2,∠B=∠C.
如图,已知∠1=∠2,∠B=∠C. 如图,已知线段a、b、c,用圆规和直尺作线段,使它等于a+2b-c.
如图,已知线段a、b、c,用圆规和直尺作线段,使它等于a+2b-c.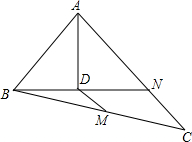 如图,在△ABC中,∠BAC=90°,AB=6,AC=8,N是AC上的点,且AN=AB,连接BN,作AD⊥BN于D,点M是BC上的动点,则当BM=
如图,在△ABC中,∠BAC=90°,AB=6,AC=8,N是AC上的点,且AN=AB,连接BN,作AD⊥BN于D,点M是BC上的动点,则当BM= 如图,在?ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①∠OBE=
如图,在?ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①∠OBE=