题目内容
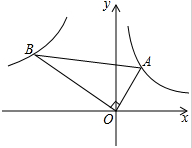 如图,已知第一象限内的点A在反比例函数y=
如图,已知第一象限内的点A在反比例函数y=| 1 |
| x |
| k |
| x |
考点:相似三角形的判定与性质,反比例函数系数k的几何意义
专题:
分析:作BF⊥x轴,AG⊥x轴,易证△OAG∽△BOF,根据OB:OA即可求得OF•BF的值,即可求得k的值,即可解题.
解答:解:作BF⊥x轴,AG⊥x轴,

∵∠BOF+∠AOG=90°,∠AOG+∠OAG=90°,
∴∠BOF=∠OAG,
∵∠BFO=∠OGA=90°,
∴△OAG∽△BOF,
∵OB:OA=3:1,
∴
=9,
∴
=9,
∴|x•
|=9,
∵反比例函数y=
在第二象限内,
∴k=-9.
故答案为:-9.

∵∠BOF+∠AOG=90°,∠AOG+∠OAG=90°,
∴∠BOF=∠OAG,
∵∠BFO=∠OGA=90°,
∴△OAG∽△BOF,
∵OB:OA=3:1,
∴
| S△OBF |
| S△AOG |
∴
| OF•BF |
| OG•GA |
∴|x•
| k |
| x |
∵反比例函数y=
| k |
| x |
∴k=-9.
故答案为:-9.
点评:本题考查了相似三角形的判定,考查了相似三角形面积比等于相似比的平方的性质,本题中求证△OAG∽△BOF是解题的关键.

练习册系列答案
相关题目
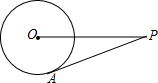 如图,P是⊙O外的一点,PA是⊙O的切线,若PO=13,PA=12,则⊙O的面积和周长分别为( )
如图,P是⊙O外的一点,PA是⊙O的切线,若PO=13,PA=12,则⊙O的面积和周长分别为( )| A、5π,10π |
| B、10π,5π |
| C、25π,10π |
| D、10π,25π |
 在平面直角坐标系xOy中,直线y=-
在平面直角坐标系xOy中,直线y=-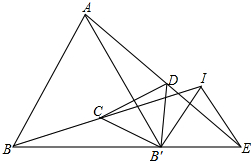 如图,已知△ABB′与△IB′E是等边三角形,连接AE、BI,C、D分别为BI、AE的中点,求证:△CDB′是等边三角形.
如图,已知△ABB′与△IB′E是等边三角形,连接AE、BI,C、D分别为BI、AE的中点,求证:△CDB′是等边三角形. 已知,如图,D为△ABC的边BC的中点,O为AD上的任一点,CD的延长线交AB于点E,BD的延长线交AC于点F,求证:EF∥BC.
已知,如图,D为△ABC的边BC的中点,O为AD上的任一点,CD的延长线交AB于点E,BD的延长线交AC于点F,求证:EF∥BC.