题目内容
9.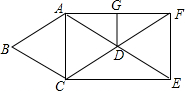 如图,在菱形ABCD中,∠B=60°,AB=1,延长AD到点E,使DE=AD,延长CD到点F,使DF=CD,连接AC、CE、EF、AF,则下列描述正确的是( )
如图,在菱形ABCD中,∠B=60°,AB=1,延长AD到点E,使DE=AD,延长CD到点F,使DF=CD,连接AC、CE、EF、AF,则下列描述正确的是( )| A. | 四边形ACEF是平行四边形,它的周长是4 | |
| B. | 四边形ACEF是矩形,它的周长是2+2$\sqrt{3}$ | |
| C. | 四边形ACEF是平行四边形,它的周长是4$\sqrt{3}$ | |
| D. | 四边形ACEF是矩形,它的周长是4+4$\sqrt{3}$ |
分析 首先判断其是平行四边形,然后判定其是矩形,然后根据菱形的边长求得矩形的周长即可.
解答 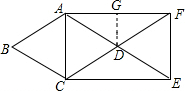 解:∵DE=AD,DF=CD,
解:∵DE=AD,DF=CD,
∴四边形ACEF是平行四边形,
∵四边形ABCD为菱形,
∴AD=CD,
∴AE=CF,
∴四边形ACEF是矩形,
∵△ACD是等边三角形,
∴AC=1,
∴EF=AC=1,
过点D作DG⊥AF于点G,则AG=FG=AD×cos30°=$\frac{\sqrt{3}}{2}$,
∴AF=CE=2AG=$\sqrt{3}$,
∴四边形ACEF的周长为:AC+CE+EF+AF=1+$\sqrt{3}$+1+$\sqrt{3}$=2+2$\sqrt{3}$,
故选B.
点评 本题考查了菱形的性质、平行四边形的判定与性质及矩形的判定与性质的知识,解题的关键是了解有关的判定定理,难度不大.

练习册系列答案
相关题目
19.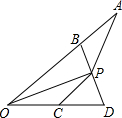 如图,OP平分∠AOD,B、C分别是OA、OD上的点,且OB≠OC,AB=CD,PC=AP,则下列结论中一定成立的个数有( )
如图,OP平分∠AOD,B、C分别是OA、OD上的点,且OB≠OC,AB=CD,PC=AP,则下列结论中一定成立的个数有( )
①S△ABP=S△PCD;②OP=BP;③∠AOD+∠APC=180°;④AO+OC=2OB.
 如图,OP平分∠AOD,B、C分别是OA、OD上的点,且OB≠OC,AB=CD,PC=AP,则下列结论中一定成立的个数有( )
如图,OP平分∠AOD,B、C分别是OA、OD上的点,且OB≠OC,AB=CD,PC=AP,则下列结论中一定成立的个数有( )①S△ABP=S△PCD;②OP=BP;③∠AOD+∠APC=180°;④AO+OC=2OB.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.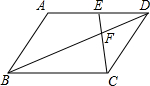 在平行四边形ABCD中,点E是边AD上一点,且AE=2ED,EC交对角线BD于点F,则$\frac{EF}{FC}$等于( )
在平行四边形ABCD中,点E是边AD上一点,且AE=2ED,EC交对角线BD于点F,则$\frac{EF}{FC}$等于( )
 在平行四边形ABCD中,点E是边AD上一点,且AE=2ED,EC交对角线BD于点F,则$\frac{EF}{FC}$等于( )
在平行四边形ABCD中,点E是边AD上一点,且AE=2ED,EC交对角线BD于点F,则$\frac{EF}{FC}$等于( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
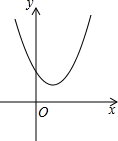 如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(0,3),且当x=1时,y有最小值2.
如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(0,3),且当x=1时,y有最小值2.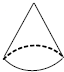 如图是一个圆锥,下列平面图形既不是它的三视图,也不是它的侧面展开图的是( )
如图是一个圆锥,下列平面图形既不是它的三视图,也不是它的侧面展开图的是( )