题目内容
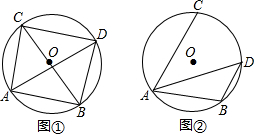
 已知?ABCD的周长为28cm,对角线AC、BD相交于点O,且△OAB的周长比△OBC的周长大4cm,且∠A=30°,求?ABCD的面积.
已知?ABCD的周长为28cm,对角线AC、BD相交于点O,且△OAB的周长比△OBC的周长大4cm,且∠A=30°,求?ABCD的面积.考点:平行四边形的性质,含30度角的直角三角形
专题:
分析:过D作DE⊥AB于E,根据平行四边形的性质得出AD=BC,DC=AB,AO=OC,OB=OD,求出AB和BC的长,求出AD,求出高DE,根据面积公式求出即可.
解答: 解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,
∴AD=BC,DC=AB,AO=OC,OB=OD,
∵?ABCD的周长为28cm,
∴AB+BC=28cm÷2=14cm,
∵△OAB的周长比△OBC的周长大4cm,
∴(OA+OB+AB)-(OB+OC+BC)=4cm,
解得:AB=9cm,BC=5cm,
则AD=BC=5cm,
过D作DE⊥AB于E,
∴∠DEA=90°,
∵∠DAB=30°,
∴DE=
AD=2.5,
∴?ABCD的面积是AB∥DE=9cm×2.5cm=22.5cm2.
 解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,∴AD=BC,DC=AB,AO=OC,OB=OD,
∵?ABCD的周长为28cm,
∴AB+BC=28cm÷2=14cm,
∵△OAB的周长比△OBC的周长大4cm,
∴(OA+OB+AB)-(OB+OC+BC)=4cm,
解得:AB=9cm,BC=5cm,
则AD=BC=5cm,
过D作DE⊥AB于E,
∴∠DEA=90°,
∵∠DAB=30°,
∴DE=
| 1 |
| 2 |
∴?ABCD的面积是AB∥DE=9cm×2.5cm=22.5cm2.
点评:本题考查了平行四边形的性质,含30度角的直角三角形的性质的应用,注意:平行四边形的对边相等,对角线互相平分.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
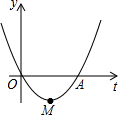 如图,抛物线y=x2+bx+c过原点,且与x轴交于A(4,0),M为抛物线的顶点,问抛物线是否存在点P,使得∠POM=90°?若存在,求出点P坐标;若不存在,说明理由.
如图,抛物线y=x2+bx+c过原点,且与x轴交于A(4,0),M为抛物线的顶点,问抛物线是否存在点P,使得∠POM=90°?若存在,求出点P坐标;若不存在,说明理由.