Question

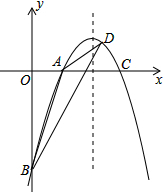如图，已知二次函数y=-

1

2

x2+bx+c的图象与x轴交于点A，与y轴交于点B，二次函数的对称轴与x轴交于点C（4，0），且tan∠OBC=

2

3

．
（1）求此二次函数的解析式；
（2）延长BC交抛物线于D，连接AB、AD，求△ABD的面积．

Answer 1

考点：待定系数法求二次函数解析式,二次函数的性质

专题：计算题

分析：（1）根据正切的定义得到tan∠OBC=

OC

OB

=

2

3

，则OB=6，所以B点坐标为（0，-6），把B点坐标代入二次函数解析式可得c=-6；利用抛物线的对称轴方程可得b=4，从而可确定抛物线解析式；
（2）先利用待定系数法求出直线BC的解析式为y=

3

2

x-6，再根据二次函数图象与一次函数图象的交点问题解方程组

y= 3 2 x-6 y=- 1 2 x2+4x-6

得到D点坐标为（5，

3

2

），根据抛物线与x轴的交点问题求出A点坐标，然后利用S_△ABD=S_△ADC+S_△ABC进行计算．

解答：解：（1）在Rt△OBC中，OC=4，
∵tan∠OBC=

OC

OB

=

2

3

，
∴OB=6，
∴B点坐标为（0，-6），
∴c=-6，
∵抛物线的对称轴为直线x=4，
∴-

b

2×(- 1 2 )

=4，解得b=4，
∴二次函数解析式为y=-

1

2

x²+4x-6；

（2）设BC的直线解析式为y=mx+n，
把B（0，-6），C（4，0）代入得

n=-6 4m+n=0

，解得

m= 3 2 n=-6

，
∴直线BC的解析式为y=

3

2

x-6，
解方程组

y= 3 2 x-6 y=- 1 2 x2+4x-6

得

x=0 y=-6

或

x=5 y= 3 2

，
∴D点坐标为（5，

3

2

），
∵方程-

1

2

x²+4x-6的解为x₁=2，x₂=6，
∴A点坐标为（2，0），
∴S_△ABD=S_△ADC+S_△ABC=

1

2

×（4-2）×

3

2

+

1

2

×（4-2）×6=

15

2

．

点评：本题考查了待定系数法求二次函数的解析式：在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解．一般地，当已知抛物线上三点时，常选择一般式，用待定系数法列三元一次方程组来求解；当已知抛物线的顶点或对称轴时，常设其解析式为顶点式来求解；当已知抛物线与x轴有两个交点时，可选择设其解析式为交点式来求解．