题目内容
19.(1)化简:$9(\sqrt{\frac{1}{3}}-\sqrt{8})+3\sqrt{3}$;(2)解方程:(2x-1)(x-3)-(x-3)2=0.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)利用因式分解法解方程.
解答 解:(1)原式=3$\sqrt{3}$-18$\sqrt{2}$+3$\sqrt{3}$
=6$\sqrt{3}$-18$\sqrt{2}$;
(2)(x-3)(2x-1-x+3)=0,
x-3=0或2x-1-x+3=0,
所以x1=3,x2=-2.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了二次根式的加减运算.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
8.若三条线段a、b、c满足a2+c2=b2,这三条线段组成的三角形是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 对角三角形 | D. | 无法判断 |
 如图,装卸工人要把放在地面上的油桶(横截面为⊙0,半径为30cm)搬运到一辆汽车上,装卸工人先在车厢顶端C处与地平面1之间用木板搭起一个坡角为60°的斜坡BC,斜坡底端为点B,工人把油桶滚到地面A处,使它紧靠在斜坡BC的Q点上,然后用力把油桶沿斜坡推上汽车,最后使油桶停放在车厢的水平面的D处⊙01的位置,此时油桶紧靠在车厢的后挡板EF上,已知汽车车厢长CE=3.3m,车厢顶端C距离地平而1.5m,求油桶从A处滚动到D处圆心所滚过的路程(结果精确列0.1m).参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1,73,π≈3.14.
如图,装卸工人要把放在地面上的油桶(横截面为⊙0,半径为30cm)搬运到一辆汽车上,装卸工人先在车厢顶端C处与地平面1之间用木板搭起一个坡角为60°的斜坡BC,斜坡底端为点B,工人把油桶滚到地面A处,使它紧靠在斜坡BC的Q点上,然后用力把油桶沿斜坡推上汽车,最后使油桶停放在车厢的水平面的D处⊙01的位置,此时油桶紧靠在车厢的后挡板EF上,已知汽车车厢长CE=3.3m,车厢顶端C距离地平而1.5m,求油桶从A处滚动到D处圆心所滚过的路程(结果精确列0.1m).参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1,73,π≈3.14. 如图所示,在△ABC中,已知∠B,∠C的平分线相交于点D,设∠A和∠BDC的度数分别为x和y,求y与x之间的函数关系式,并求x的取值范围.
如图所示,在△ABC中,已知∠B,∠C的平分线相交于点D,设∠A和∠BDC的度数分别为x和y,求y与x之间的函数关系式,并求x的取值范围.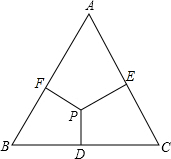 如图,P为正三角形ABC内任一点,PD⊥BC,PE⊥CA,PF⊥AB,则$\frac{PD+PE+PF}{BD+CE+AF}$=$\frac{\sqrt{3}}{3}$.
如图,P为正三角形ABC内任一点,PD⊥BC,PE⊥CA,PF⊥AB,则$\frac{PD+PE+PF}{BD+CE+AF}$=$\frac{\sqrt{3}}{3}$.