题目内容
7.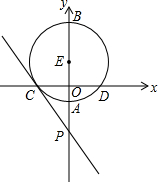 如图,在平面直角坐标系中,以E(0,1)为圆心,3为半径的⊙E交y轴于A、B两点,交x轴于C、D两点,点P的坐标为(0,-8)
如图,在平面直角坐标系中,以E(0,1)为圆心,3为半径的⊙E交y轴于A、B两点,交x轴于C、D两点,点P的坐标为(0,-8)(1)直接写出A,B,C三点的坐标:(0,-2);(0,4);(-2$\sqrt{2}$,0);
(2)求证:PC是⊙E的切线.
分析 (1)连接CE,分别求出OC,OA,OB的长,即可求出点C,点A,点B的坐标;
(2)利用勾股定理的逆定理证明∠ECP=90°即可证明PC是⊙E的切线.
解答 解:
(1)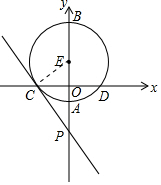 连接CE,
连接CE,
∵圆E的半径为3,(0,1)为圆心,
∴OE=1,OA=2,CE=3,
∴OC=$\sqrt{C{E}^{2}-O{E}^{2}}$=2$\sqrt{2}$,
∵OE⊥CD,
∴OD=CD=2$\sqrt{2}$,
∴AB=6,
∴OB=6-2=4,
∴点A,B,C三点的坐标分别为:(0,-2);(0,4);(-2$\sqrt{2}$,0),
故答案为:(0,-2);(0,4);(-2$\sqrt{2}$,0);
(2)证明:
∵点P的坐标为(0,-8),
∴OP=8,
∵OC=2$\sqrt{2}$,
∴PC=$\sqrt{O{C}^{2}+O{P}^{2}}$=6$\sqrt{2}$,
∵PE=9,CE=3,
∴PC2+CE2=PE2,
∴△ECP是直角三角形,
∴∠ECP=90°,
∴CE⊥PC,
∴PC是⊙E的切线.
点评 本题主要考查了切线的判定定理运用、垂径定理的运用以及勾股定理以及其逆定理的运用,熟练掌握和圆有关的各种性质是解题的关键.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
17.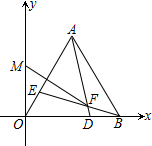 如图,在平面直角坐标系中,等边△OAB的边OB在x轴正半轴上,点A(3,m),m>0,点D、E分别从B、O以相同的速度向O、A运动,连接AD、BE,交点为F,M是y轴上一点,则FM的最小值是( )
如图,在平面直角坐标系中,等边△OAB的边OB在x轴正半轴上,点A(3,m),m>0,点D、E分别从B、O以相同的速度向O、A运动,连接AD、BE,交点为F,M是y轴上一点,则FM的最小值是( )
 如图,在平面直角坐标系中,等边△OAB的边OB在x轴正半轴上,点A(3,m),m>0,点D、E分别从B、O以相同的速度向O、A运动,连接AD、BE,交点为F,M是y轴上一点,则FM的最小值是( )
如图,在平面直角坐标系中,等边△OAB的边OB在x轴正半轴上,点A(3,m),m>0,点D、E分别从B、O以相同的速度向O、A运动,连接AD、BE,交点为F,M是y轴上一点,则FM的最小值是( )| A. | 3 | B. | $\sqrt{3}$+1 | C. | 2$\sqrt{3}$-2 | D. | 6-2$\sqrt{3}$ |
 在数学活动课上,老师带领学生去测量操场上树立的旗杆的高度,老师为同学们准备了如下工具:①高为m米的测角仪,②长为n米的竹竿,③足够长的皮尺.请你选用以上的工具,设计一个可以通过测量,求出国旗杆高度的方案(不用计算和说明,画出图形并标记可以测量的长度或者角度即可,可测量的角度选用α,β,γ标记,可测量的长度选用a,b,c,d标记,测角仪和竹竿可以用线段表示).
在数学活动课上,老师带领学生去测量操场上树立的旗杆的高度,老师为同学们准备了如下工具:①高为m米的测角仪,②长为n米的竹竿,③足够长的皮尺.请你选用以上的工具,设计一个可以通过测量,求出国旗杆高度的方案(不用计算和说明,画出图形并标记可以测量的长度或者角度即可,可测量的角度选用α,β,γ标记,可测量的长度选用a,b,c,d标记,测角仪和竹竿可以用线段表示).
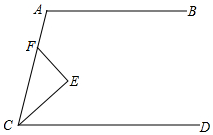 如图,AB∥CD,CE平分∠ACD,∠A=110°,F是AC上一点,∠AFE=125°,求证:FE⊥CE.
如图,AB∥CD,CE平分∠ACD,∠A=110°,F是AC上一点,∠AFE=125°,求证:FE⊥CE.