题目内容
7.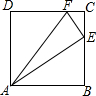 已知正方形ABCD中,AB=5,E是BC上的一点,连接AE,过点E作EF⊥AE,交CD于点F.当E点在BC边上运动时,设线段BE的长为x,线段CF的长为y.
已知正方形ABCD中,AB=5,E是BC上的一点,连接AE,过点E作EF⊥AE,交CD于点F.当E点在BC边上运动时,设线段BE的长为x,线段CF的长为y.(Ⅰ)求y关于x的函数解析式及其定义域;
(Ⅱ)根据(Ⅰ)中所得y关于x的函数图象,求当BE的长为何值时,线段CF最长,并求此时CF的长.
分析 (Ⅰ)由题意易得△CEF∽△BAE,根据对应边成比例,可得y关于x的函数解析式,根据BC的长确定定义域即可;
(Ⅱ)用配方法求得二次函数的最值即可.
解答 解:(Ⅰ)∵四边形ABCD是正方形,
∴∠B=90°,
∵EF⊥AE,
∴∠AEF=90°.
又∵∠CEA=∠CEF+∠AEF,∠CEA=∠BAE+∠B,
∴∠CEF=∠BAE,
又∵∠B=∠C=90°,
∴△CEF∽△BAE,
∴$\frac{CF}{BE}$=$\frac{CE}{AB}$,
∴$\frac{y}{x}$=$\frac{5-x}{x}$,
∴y=-$\frac{1}{5}$x2+x(0<x<5);
(Ⅱ)y=-$\frac{1}{5}$x2+x=-$\frac{1}{5}$(x-$\frac{5}{2}$)2$+\frac{5}{4}$
根据函数图象可知,抛物线y=-$\frac{1}{5}$x2+x=-$\frac{1}{5}$(x-$\frac{5}{2}$)2$+\frac{5}{4}$,
开口向下,抛物线的顶点坐标是它的最高点、且x=$\frac{5}{2}$在函数的定义域内.
所以当BE的长为$\frac{5}{2}$时,CF的长最大为$\frac{5}{4}$.
点评 此题考查了相似三角形的判定及性质的应用、二次函数的最值求法、直角三角形中锐角函数值的求法等知识点.

练习册系列答案
相关题目
17.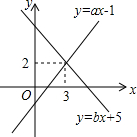 一次函数y=ax-1和y=bx+5的图象如图所示,则a、b的值是( )
一次函数y=ax-1和y=bx+5的图象如图所示,则a、b的值是( )
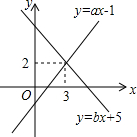 一次函数y=ax-1和y=bx+5的图象如图所示,则a、b的值是( )
一次函数y=ax-1和y=bx+5的图象如图所示,则a、b的值是( )| A. | a=3,b=2 | B. | a=2,b=3 | C. | a=1,b=-1 | D. | a=-1,b=1 |
2.已知一元二次方程ax2+bx+c=0(a≠0)中,下列命题是真命题的有( )
①若a+b+c=0,则b2-4ac≥0
②若方程ax2+bx+c=0两根为1和2,则2a+c=0;
③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根.
①若a+b+c=0,则b2-4ac≥0
②若方程ax2+bx+c=0两根为1和2,则2a+c=0;
③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 0个 |
12.某服装店原计划按每套200元的价格销售一批保暖内衣,但上市后销售不佳,为减少库存积压,两次连续降价打折处理,最后价格调整为每套128元.若两次降价折扣率相同,则每次降价率为( )
| A. | 8% | B. | 18% | C. | 20% | D. | 25% |
16.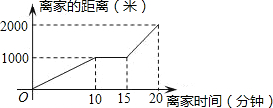 某天小明骑自行车上学,途中因发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.如图描述了他上学的情景,下列说法中错误的是( )
某天小明骑自行车上学,途中因发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.如图描述了他上学的情景,下列说法中错误的是( )
 某天小明骑自行车上学,途中因发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.如图描述了他上学的情景,下列说法中错误的是( )
某天小明骑自行车上学,途中因发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.如图描述了他上学的情景,下列说法中错误的是( )| A. | 学校离家的距离为1000米 | |
| B. | 修车时间为5分钟 | |
| C. | 到达学校时共用时间20分钟 | |
| D. | 修车后小明骑车的速度是修车前速度的2倍 |
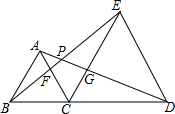 如图,△ABC和△ECD都是等边三角形,连接BE和AD,AC交BE于点F,AD交CE于点G,AD交BE于点P.
如图,△ABC和△ECD都是等边三角形,连接BE和AD,AC交BE于点F,AD交CE于点G,AD交BE于点P.