题目内容
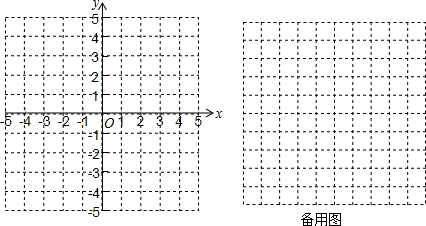
12.一束光线从y轴上点A(0,2)出发,经过x轴上某点C反射后经过点B(6,6),光线从A点到B点所经过的路线长为10.分析 根据题意可以先画出相应的图形,根据入射角等于反射角,三角形的相似,勾股定理,可以解答本题.
解答 解:如下图似乎所示:
点一束光线从点A出发,与x轴交于点C,反射后经过点B,作BD⊥x轴于点D,
∵入射角等于反射角,
∴∠ACO=∠BCD.
∵∠AOC=∠BDC,
∴△ACO∽△BCD.
设OC=x,则CD=6-x.
∴$\frac{OC}{OA}=\frac{DC}{DB}$.
∵点A(0,2),点B(6,6),
∴$\frac{x}{2}=\frac{6-x}{6}$.
解得x=1.5.
∴AC=$\sqrt{{2}^{2}+1.{5}^{2}}=\sqrt{6.25}=2.5$,BC=$\sqrt{(6-1.5)^{2}+{6}^{2}}=\sqrt{7.{5}^{2}}=7.5$.
∴光线从A点到B点所经过的路线长为:AC+CB=2.5+7.5=10.
故答案为:10.
点评 本题考查坐标与图形的性质、入射角等于反射角、三角形相似、勾股定理,解题的关键是能根据题意画出相应的图形.

练习册系列答案
相关题目
1.如图,边长为m+4的正方形纸片剪出一个边长为m的正方形之后,剩余部分可剪拼成一个矩形,若拼成的矩形一边长为4,则另一边长为( )
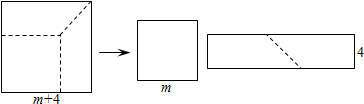

| A. | m+4 | B. | 2m+4 | C. | m+8 | D. | 2m-4 |
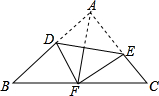 如图,将△ABC沿DE折叠,使点A与BC边的中点F重合,下列结论中:①EF∥AB且EF=$\frac{1}{2}$AB;②∠BAF=∠CAF;③S四边形ADFE=$\frac{1}{2}$S△ABC;④∠BDF+∠FEC=2∠BAC,正确的是④(把你认为正确的都填上,成立的说明理由).
如图,将△ABC沿DE折叠,使点A与BC边的中点F重合,下列结论中:①EF∥AB且EF=$\frac{1}{2}$AB;②∠BAF=∠CAF;③S四边形ADFE=$\frac{1}{2}$S△ABC;④∠BDF+∠FEC=2∠BAC,正确的是④(把你认为正确的都填上,成立的说明理由).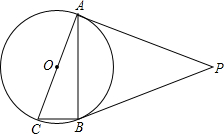 如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB.
如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB. 如图,将长方形纸片ABCD沿AE向上折叠,使点B落在DC边上的F点处,若△AFD的周长为9,△FCE的周长为3,则长方形ABCD的周长为12.
如图,将长方形纸片ABCD沿AE向上折叠,使点B落在DC边上的F点处,若△AFD的周长为9,△FCE的周长为3,则长方形ABCD的周长为12.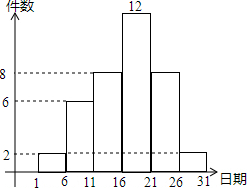 在学校开展的综合实践活动中,八年级某班对本班的40名学生进行了小制作评比,作品上交时间为5月1日至31日,评委把同学们上交作品的件数按5天一组分组统计,绘制了频数直方图(如图),图中从左到右依次为第一、二、三、四、五、六组.
在学校开展的综合实践活动中,八年级某班对本班的40名学生进行了小制作评比,作品上交时间为5月1日至31日,评委把同学们上交作品的件数按5天一组分组统计,绘制了频数直方图(如图),图中从左到右依次为第一、二、三、四、五、六组.