题目内容
3. 已知直线l1:y1=x+m与直线l2:y2=nx+3相交于点A(1,2).
已知直线l1:y1=x+m与直线l2:y2=nx+3相交于点A(1,2).(1)求m、n的值;
(2)设l1交x轴于点B,l2交x轴于点C,若点D与点A,B,C能构成平行四边形,请直接写出D点坐标;
(3)请在所给坐标系中画出直线l1和l2,并根据图象回答问题:
当x满足x>1时,y1>2;
当x满足0≤x<3时,0<y2≤3;
当x满足x<1时,y1<y2.
分析 (1)根据待定系数法即可求得;
(2)根据平行四边形的性质求得即可;
(3)根据图象求得即可.
解答 解:(1)将点A(1,2)代入y1=x+m与y2=nx+3得2=1+m,2=n+3,
解得 m=1,n=-1;
(2)由直线l1:y1=x+1与直线l2:y2=-x+3可知:l1交x轴于点B(-1,0),l2交x轴于点C(3,0),如图:
∵点D与点A,B,C能构成平行四边形,
∴D的坐标为(5,2)或(-3,2)或(1,-2);
(3)根据图象可知:当x满足x>1时,y1>2;当x满足0≤x<3时,0<y2≤3;
当x满足x<1时,y1<y2.
故答案为:x>1、0≤x<3、x<1.
点评 本题考查了两条直线相交或平行问题以及待定系数法求一次函数的解析式,两条直线的交点坐标,一次函数和一次不等式的关系,关键是掌握凡是函数图象经过的点必能满足解析式.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
11. 如图,⊙O半径为2,AB为⊙O的直径,BC为⊙O的一条弦,若∠ABC=30°,过点C作AB的垂线,垂足为点D,则CD长为( )
如图,⊙O半径为2,AB为⊙O的直径,BC为⊙O的一条弦,若∠ABC=30°,过点C作AB的垂线,垂足为点D,则CD长为( )
 如图,⊙O半径为2,AB为⊙O的直径,BC为⊙O的一条弦,若∠ABC=30°,过点C作AB的垂线,垂足为点D,则CD长为( )
如图,⊙O半径为2,AB为⊙O的直径,BC为⊙O的一条弦,若∠ABC=30°,过点C作AB的垂线,垂足为点D,则CD长为( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | 2 | D. | 1 |
8.下列各数中:+(-5)、|-1-2|、-$\frac{π}{2}$、-(-7)、0、(-2015)3,负数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
 如图,已知函数y1=$\frac{4}{x}$,y2=$\frac{k}{x}$在第一象限的图象.过函数y1=$\frac{4}{x}$的图象上的任意
如图,已知函数y1=$\frac{4}{x}$,y2=$\frac{k}{x}$在第一象限的图象.过函数y1=$\frac{4}{x}$的图象上的任意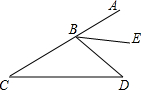 如图,在△BCD中,∠C=30°,∠D=40°,点A为CB的延长线上一点,BE为∠ABD的角平分线,则∠ABE=35°.
如图,在△BCD中,∠C=30°,∠D=40°,点A为CB的延长线上一点,BE为∠ABD的角平分线,则∠ABE=35°. 如图,矩形纸片ABCD的边AD=9,AB=3,将其折叠,使点D与点B重合,则折叠后DE的长为( )
如图,矩形纸片ABCD的边AD=9,AB=3,将其折叠,使点D与点B重合,则折叠后DE的长为( )