题目内容
4．在平面直角坐标系中，将抛物线y=x2+2x+3绕着点（2，1）旋转180°，所得抛物线的解析式是y=-（x-5）2．分析 根据中心对称，可得顶点坐标是（5，0），根据旋转的性质，可得答案．
解答 解：将抛物线y=x2+2x+3绕着点（2，1）旋转180°，所得抛物线的顶点坐标是（5，0），
将抛物线y=x2+2x+3绕着点（2，1）旋转180°，所得抛物线的解析式是y=-（x-5）2，
故答案为：y=-（x-5）2．
点评 本题考查了二次函数图象与几何变换，利用中心对称得出顶点坐标是解题关键．
练习册系列答案
相关题目
14．Rt△ABC中，∠C=90°，AC=3，BC=4，则中线CD的长是（ ）
| A． | 2 | B． | 2.5 | C． | 5 | D． | 1.5 |
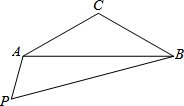如图，已知等腰三角形ABC，∠ACB=120°且AC=BC=4，在平面内任作∠APB=60°，BP最大值为8．