题目内容
9.某商品进价为每件40元,如果售价为每件50元,每个月可卖出210件,如果售价超过50元,但不超过80元,每件商品的售价每上涨10元,每个月少卖1件,如果售价超过80元后,若再涨价,每件商品的售价每涨10元,每个月少卖3件.设该商品的售价为x元.(1)每件商品的利润为多少元.若超过50元,但不超过80元,每月售几件?若超过80元,每月售几件?(用x的式子表示)
(2)若超过50元但是不超过80元,售价为多少时利润可达到7200元?
(3)若超过80元,售价为多少时利润为7500元?
分析 (1)当售价超过50元但不超过80元,每件商品的售价每上涨10元,则每个月少卖1件,则每月销售的数量为:210+$\frac{1}{10}$(x-50)=205+$\frac{1}{10}$x;当如果售价超过80元后,若再涨价,则每涨10元每月少卖3件,每月销售的数量为:210-3×$\frac{1}{10}$(x-80)=224-$\frac{3}{10}$x;
(2)(3)由利润=(售价-成本)×销售量列出方程解答即可.
解答 解:(1)依题意得:当50≤x≤80时,每月销售的数量为:210-$\frac{1}{10}$(x-50)=215-$\frac{1}{10}$x,
当80<x<140时,每月销售的数量为:210-3×$\frac{1}{10}$(x-80)=224-$\frac{3}{10}$x.
(2)由利润=(售价-成本)×销售量可以列出函数关系式,
w=-x2+300x-10400(50≤x≤80)
若超过50元但是不超过80元,售价为x时利润可达到7200元,
可列出关系式:-x2+300x-10400=7200
解得:x=80.
答:若超过50元但是不超过80元,售价为80时利润可达到7200元.
(3)当x>80时,w=-3x2+540x-16800,
若超过80元,售价为x元时利润为7500元,
可列出关系式:-3x2+540x-16800,
解得:x=90,
答:若超过80元,售价为90元时利润为7500元.
点评 本题主要考查二次函数的应用,根据不同自变量的取值范围,利用基本数量关系得出函数解析式是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.若关于x的一元二次方程kx2-2x-1=0有两个不相等的实数根,则k的取值范围是( )
| A. | k>-1 | B. | k>-1且k≠0 | C. | k<1 | D. | k<1且k≠0 |
17.下列说法中,不正确的是( )
| A. | 任意一个负实数的绝对值都是它的相反数 | |
| B. | 任意一个实数都有相反数 | |
| C. | 任意一个实数都有倒数 | |
| D. | 任意一个实数都可以在数轴上找到一点与其对应 |
4. 某校共有2425名学生,其中各年级学生所占比例如扇形统计图,则学生最多的年级有( )
某校共有2425名学生,其中各年级学生所占比例如扇形统计图,则学生最多的年级有( )
 某校共有2425名学生,其中各年级学生所占比例如扇形统计图,则学生最多的年级有( )
某校共有2425名学生,其中各年级学生所占比例如扇形统计图,则学生最多的年级有( )| A. | 873名 | B. | 1115名 | C. | 485名 | D. | 1067名 |
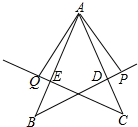 已知,如图,AB=AC,AD=AE,AP⊥BD,AQ⊥CE,垂足分别为P、Q,求证:AP=AQ.
已知,如图,AB=AC,AD=AE,AP⊥BD,AQ⊥CE,垂足分别为P、Q,求证:AP=AQ.