题目内容
14.判别下列关于x的一元二次方程的根的情况.(1)$\frac{1}{4}$x2-2mx+5m2+1=0;
(2)x2-4mx+4m2=0;
(3)$\frac{1}{2}$x2-mx+m-$\frac{1}{2}$=0;
(4)$\frac{1}{2}$x2-mx+m-4=0.
分析 根据①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;③当△<0时,方程无实数根.由此可得出答案.
解答 解:(1)$\frac{1}{4}$x2-2mx+5m2+1=0,
∵△=(-2m)2-4×$\frac{1}{4}$×(5m2+1)=-m2-1<0,
∴方程没有实数根;
(2)x2-4mx+4m2=0,
∵△=(-4m)2-4×4m2=0,
∴方程有两个相等的实数根;
(3)$\frac{1}{2}$x2-mx+m-$\frac{1}{2}$=0,
∵△=(-m)2-4×$\frac{1}{2}×$(m-$\frac{1}{2}$)=(m-1)2,
∴方程有两个的实数根;
(4)$\frac{1}{2}$x2-mx+m-4=0,
∵△=(-m)2-4×$\frac{1}{2}$×(m-4)=(m-1)2+7>0,
∴方程有两个不相等的实数根.
点评 本题考查了根的判别式,属于基础题,注意掌握根的判别式与根的个数之间的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4. 某校共有2425名学生,其中各年级学生所占比例如扇形统计图,则学生最多的年级有( )
某校共有2425名学生,其中各年级学生所占比例如扇形统计图,则学生最多的年级有( )
 某校共有2425名学生,其中各年级学生所占比例如扇形统计图,则学生最多的年级有( )
某校共有2425名学生,其中各年级学生所占比例如扇形统计图,则学生最多的年级有( )| A. | 873名 | B. | 1115名 | C. | 485名 | D. | 1067名 |
 如图,一辆小汽车从小山脚下的A点直线行驶15分钟到达山顶的B点,已知小汽车的平均速度为40千米/时,小山的高度BC约为6000米,求小山的坡比.
如图,一辆小汽车从小山脚下的A点直线行驶15分钟到达山顶的B点,已知小汽车的平均速度为40千米/时,小山的高度BC约为6000米,求小山的坡比. 根据图中标示的数据,计算图形的周长(单位:mm)
根据图中标示的数据,计算图形的周长(单位:mm) 如图,在△ABC中,BC=4,AC=6,△ABC的高AD与BE的比是多少?
如图,在△ABC中,BC=4,AC=6,△ABC的高AD与BE的比是多少?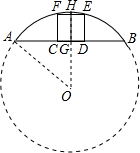 如图,四边形CDEF是弓形的内接正方形,已知弓形的弦AB长为8,弓形的高HG为2.
如图,四边形CDEF是弓形的内接正方形,已知弓形的弦AB长为8,弓形的高HG为2.