题目内容
5.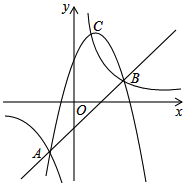 已知Y1,Y2,Y3分别表示二次函数、反比例函数和一次函数的三个函数值,它们的交点分别是A(-1,-2)、B(2,1)和C($\frac{2}{3}$,3),规定M={Y1,Y2,Y3}中最小的函数值,则下列结论:①当x<-1时,M=Y1;②当-1<x<0时,Y2<Y3<Y1;③当0≤x≤2时,M的最大值是1,无最小值;④当x≥2时,M最大值是1,无最小值.其中正确结论的个数为①②④.(填序号即可)
已知Y1,Y2,Y3分别表示二次函数、反比例函数和一次函数的三个函数值,它们的交点分别是A(-1,-2)、B(2,1)和C($\frac{2}{3}$,3),规定M={Y1,Y2,Y3}中最小的函数值,则下列结论:①当x<-1时,M=Y1;②当-1<x<0时,Y2<Y3<Y1;③当0≤x≤2时,M的最大值是1,无最小值;④当x≥2时,M最大值是1,无最小值.其中正确结论的个数为①②④.(填序号即可)
分析 首先要明确M={Y1,Y2,Y3中最小的函数值},观察图象可以判断四个题目的正误.
解答 解:一次函数Y3过点A(-1,-2)、B(2,1),则解析式为:Y3=x-1;
①当x<-1时,Y1,Y2,Y3中最小的函数值为Y1,所以M=Y1,故①正确;
②当-1<x<0时,Y2<Y3<Y1,故②正确;
③当0≤x≤2时,Y1,Y2,Y3中最小的函数值为Y3,M的最小值是-1,最大值是1;故③错误;
④当x≥2时,Y1,Y2,Y3中最小的函数值为Y1,则M最大值是1,无最小值,故④正确.
故选:①②④.
点评 本题综合考查了二次函数、一次函数、反比例函数的性质,同时此类题考查了学生能根据图象求最值问题,这在学生中是一个难点,原则是:在一定范围内,最下边是最小,最上边是最大.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
15.下列命题中,真命题的个数是( )
①若x≠0,则x2>0;
②如果两个角互补,那么这两个角一个是锐角一个是钝角;
③一个角的补角大于这个角;
④两条直线被第三条直线所截,同位角相等.
①若x≠0,则x2>0;
②如果两个角互补,那么这两个角一个是锐角一个是钝角;
③一个角的补角大于这个角;
④两条直线被第三条直线所截,同位角相等.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
17.如果a=(-6)-1,b=(-2)0,c=(-3)2,那么a、b、c三数的大小为( )
| A. | a>b>c | B. | c>a>b | C. | a>c>b | D. | c>b>a |
14.计算$\frac{{a}^{2}}{{b}^{3}}$÷$\frac{a}{2b}$的结果是( )
| A. | $\frac{2a}{b}$ | B. | $\frac{a}{{b}^{2}}$ | C. | $\frac{a}{{2b}^{2}}$ | D. | $\frac{2a}{{b}^{2}}$ |
15.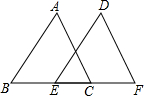 如图,E、B、F、C四点在同一条直线上,EB=CF,∠DEF=∠ABC,添加以下哪一个条件不能判断△ABC≌△DEF的是( )
如图,E、B、F、C四点在同一条直线上,EB=CF,∠DEF=∠ABC,添加以下哪一个条件不能判断△ABC≌△DEF的是( )
 如图,E、B、F、C四点在同一条直线上,EB=CF,∠DEF=∠ABC,添加以下哪一个条件不能判断△ABC≌△DEF的是( )
如图,E、B、F、C四点在同一条直线上,EB=CF,∠DEF=∠ABC,添加以下哪一个条件不能判断△ABC≌△DEF的是( )| A. | ∠A=∠D | B. | DF∥AC | C. | AC=DF | D. | AB=DE |