题目内容
9.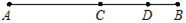 如图,点C是线段AB上一点,D是线段CB的中点,已知图中所有的线段的长度之和为23,线段AC的长度与线段CB的长度都是正整数,则线段AC长3.
如图,点C是线段AB上一点,D是线段CB的中点,已知图中所有的线段的长度之和为23,线段AC的长度与线段CB的长度都是正整数,则线段AC长3.
分析 可以设出AC和CD的长,再根据图中所有线段的长度之和为23,即可列出等式,再根据线段AC的长度与线段CB的长度都是正整数,即可求出答案.
解答 解:设AC=y,CD=BD=x,则AC+CD+DB+AD+AB+CB=23,
即:y+x+x+(x+y)+(2x+y)+2x=23,
得:7x+3y=23,
因为线段AC的长度与线段CB的长度都是正整数,
所以可知x最大为3,
可知:x=3,y为小数,不符合;
x=2,y=3,符合题意;
x=1,y为小数,不符合.
所以AC=3,
故答案为:3.
点评 本题考查了比较线段长短的知识,有一定难度,根据题意列出方程式,并探讨解的合理性是关键.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
19.下列各数中,互为相反数的是( )
| A. | -2与(-2)2 | B. | -2与2 | C. | -2与-$\frac{1}{2}$ | D. | $\frac{1}{2}$与-2 |
17.已知一次函数y=kx+7和y=k′x+5,假设k>0且k′<0,则这两个一次函数的图象的交点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
4.点M(3,-4)关于y的轴的对称点是M1,则M1关于x轴的对称点M2的坐标为( )
| A. | (-3,4) | B. | (-3,-4) | C. | (3,4) | D. | (3,-4) |
14.若直线y=mx+n经过平面直角坐标系的第一、二、四象限,则点P(m,n)所处的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
1.大于-2.5而小于$\root{3}{46}$的整数共有( )
| A. | 7个 | B. | 6个 | C. | 5个 | D. | 4个 |
19.点P在半径为r的⊙A外,则点P到点A的距离d与r的关系是( )
| A. | d≤r | B. | d<r | C. | d≥r | D. | d>r |
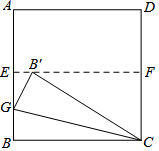 如图,四边形ABCD是一张正方形纸片,先将正方形ABCD对折,使BC与AD重合,折痕为EF,把这个正方形展平,然后沿直线CG折叠,使B点落在EF上,对应点为B′.则∠B′GC=75度.
如图,四边形ABCD是一张正方形纸片,先将正方形ABCD对折,使BC与AD重合,折痕为EF,把这个正方形展平,然后沿直线CG折叠,使B点落在EF上,对应点为B′.则∠B′GC=75度.