题目内容
13.如图,△ACD∽△A1C1D1,顶点A、D、C分别与A1、D1、C1对应,点B、B1分别在AD、A1D1、的延长线上,且AD=$\frac{1}{3}$BD,A1D1=$\frac{1}{3}$B1D1.求证:$\frac{CD}{{C}_{1}{D}_{1}}$=$\frac{BC}{{B}_{1}{C}_{1}}$.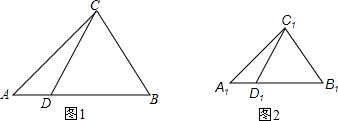
分析 由△ACD∽△A1C1D1,得到$\frac{AC}{{A}_{1}{C}_{1}}$=$\frac{AD}{{A}_{1}{D}_{1}}$,∠A=∠A1,∠ADC=∠A1D1C1,推出∠CDB=∠C1D1B1,根据已知条件AD=$\frac{1}{3}$BD,A1D1=$\frac{1}{3}$B1D1.得到AD=$\frac{1}{4}$AB,A1D1=$\frac{1}{4}$A1B1,推出△ABC∽△A1C1B1,得到∠B=∠B1,证得△CDB∽△C1D1B1,即可得到结论.
解答 解:∵△ACD∽△A1C1D1,
∴$\frac{AC}{{A}_{1}{C}_{1}}$=$\frac{AD}{{A}_{1}{D}_{1}}$,∠A=∠A1,∠ADC=∠A1D1C1,
∴∠CDB=∠C1D1B1,
∵AD=$\frac{1}{3}$BD,A1D1=$\frac{1}{3}$B1D1.
∴AD=$\frac{1}{4}$AB,A1D1=$\frac{1}{4}$A1B1,
∴$\frac{AC}{{A}_{1}{C}_{1}}$=$\frac{AB}{{A}_{1}{B}_{1}}$,
∴△ABC∽△A1C1B1,
∴∠B=∠B1,
∴△CDB∽△C1D1B1,
∴$\frac{CD}{{C}_{1}{D}_{1}}$=$\frac{BC}{{B}_{1}{C}_{1}}$.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.如果一个几何体的任何一个截面都是圆,那么这个几何体是( )
| A. | 柱体 | B. | 锥体 | C. | 正方体 | D. | 球体 |

 如图,平面直角坐标系中,直线AB与x轴,y轴分别交于A(3,0),B(0,$\sqrt{3}$)两点,点C、D分别为线段AB、OA上的一动点.
如图,平面直角坐标系中,直线AB与x轴,y轴分别交于A(3,0),B(0,$\sqrt{3}$)两点,点C、D分别为线段AB、OA上的一动点.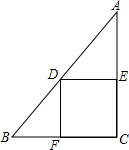 已知:如图在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF.设DE=x,四边形DECF的面积为y,则y与x之间的函数关系式为y=-2x2+8x.
已知:如图在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF.设DE=x,四边形DECF的面积为y,则y与x之间的函数关系式为y=-2x2+8x.