题目内容
5. 已知矩形ABCD的对角线相交于O,OF⊥AD,OF=2cm,AE⊥BD,且BE=OE
已知矩形ABCD的对角线相交于O,OF⊥AD,OF=2cm,AE⊥BD,且BE=OE(1)求证:AB=AO;
(2)求证:∠CAD=30°;
(3)求AC的长.
分析 (1)根据线段垂直平分线的性质即可得出结论;(2)先证明△AOB是等边三角形,求出∠BAO=60°,即可得出结果;
(3)在Rt△AOF中,根据含30°角的直角三角形的性质求出AO,即可得出AC的长.
解答 (1)证明:∵AE⊥BD,且BE=OE,
∴AB=AO;
(2)证明:∵四边形ABCD是矩形,
∴∠BAD=90°,AO=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD,
∴AO=OD,
由(1)得AB=AO,
∴AB=AO=OB,
∴∠BAO=60°,
∴∠CAD=90°-60°=30°;
(3)解:∵OF⊥AD,
∴∠AFO=90°,
又∵∠CA=30°,
∴AO=2OF=4cm,
∴AC=2AO=8cm.
点评 本题考查了矩形的性质、含30°角的直角三角形的性质以及等边三角形的判定因此性质;证明三角形是等边三角形是解决问题的关键.

练习册系列答案
相关题目
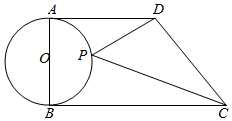 已知:AB是⊙O的直径,AD、BC是⊙O的切线,P是⊙O上一动点,若AD=5,AB=4,BC=8,则△PCD的面积的最小值是( )
已知:AB是⊙O的直径,AD、BC是⊙O的切线,P是⊙O上一动点,若AD=5,AB=4,BC=8,则△PCD的面积的最小值是( ) 如图所示,在平行四边形ABCD中,∠B=80°,AE平分∠BAD交BC于点E,DF=BE,则∠1=50°.
如图所示,在平行四边形ABCD中,∠B=80°,AE平分∠BAD交BC于点E,DF=BE,则∠1=50°.