题目内容
5. 如图所示,A、B、C为长方体的三个顶点,则△ABC的形状是( )
如图所示,A、B、C为长方体的三个顶点,则△ABC的形状是( )| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法确定 |
分析 利用勾股定理求出AB、AC、BC的长度,再利用余弦定理判断三角形的形状即可.
解答 解:设长方体的长为a,宽为b,高为c,
可得:AB2=a2+c2,BC2=b2+c2,AC2=a2+b2,
因为$cosA=\frac{A{B}^{2}+A{C}^{2}-B{C}^{2}}{2AB•AC}=\frac{{a}^{2}+{c}^{2}+{a}^{2}+{b}^{2}-{b}^{2}-{c}^{2}}{2\sqrt{{a}^{2}+{b}^{2}}•\sqrt{{a}^{2}+{c}^{2}}}$<1,
所以∠A是锐角,
同理可得∠B与∠C是锐角,
所以此三角形的锐角三角形,
故选A.
点评 本题主要考查了三角形的形状判断,其关键是要根据勾股定理计算出三角形的边长,进一步根据余弦定理进行判断.

练习册系列答案
相关题目
14.如果多项式x2+ax+b可因式分解为(x-1)(x+2),则a、b的值为( )
| A. | a=1,b=2 | B. | a=1,b=-2 | C. | a=-1,b=-2 | D. | a=-1,b=2 |

 C. -5 D. -
C. -5 D. -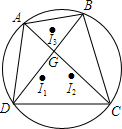 如图,四边形ABCD内接于圆,对角线AC、BD交于点G,I1、I2、I3分别为△ADC、△BDC、△ABG的内心.证明:I3G⊥I1I2.
如图,四边形ABCD内接于圆,对角线AC、BD交于点G,I1、I2、I3分别为△ADC、△BDC、△ABG的内心.证明:I3G⊥I1I2.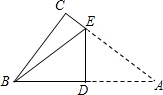 如图,Rt△ABC中,∠C=90°,BC=4,AC=6,现将△ABC沿ED翻折,使点A与点B重合,折痕为DE,则tan∠BED的值是$\frac{3}{2}$.
如图,Rt△ABC中,∠C=90°,BC=4,AC=6,现将△ABC沿ED翻折,使点A与点B重合,折痕为DE,则tan∠BED的值是$\frac{3}{2}$.