题目内容
20.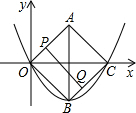 已知:四边形AOBC是正方形,C点的坐标是$(4\sqrt{2},0)$,动点P、Q同时从O点出发,P沿折线OACB的方向运动,Q沿折线OBCA的方向运动.若P的运动速度是每秒1个单位长度,Q的运动速度是每秒2个单位长度,运动到相遇时停止,设△OPQ的面积为S,运动时间为t秒,则S与t之间的函数图象大致是( )
已知:四边形AOBC是正方形,C点的坐标是$(4\sqrt{2},0)$,动点P、Q同时从O点出发,P沿折线OACB的方向运动,Q沿折线OBCA的方向运动.若P的运动速度是每秒1个单位长度,Q的运动速度是每秒2个单位长度,运动到相遇时停止,设△OPQ的面积为S,运动时间为t秒,则S与t之间的函数图象大致是( )| A. |  | B. | 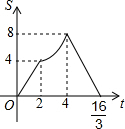 | C. | 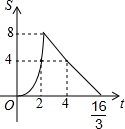 | D. | 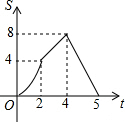 |
分析 本问实际上是一个分段函数,P、Q到达不同的位置S与t的解析式是不一样的,Q到达B点时P在OA的中点,Q到达C点时P到达A点,求出P、Q的 相遇时间分3种情况就可以表示出其函数关系式.
解答 解:由题意得:t+2t=16
解得:t=$\frac{16}{3}$
∴PQ相遇的时间为$\frac{16}{3}$在整个运动过程中S与t的函数关系式有三种情况:
①当0≤t≤2时,S=$\frac{1}{2}t•2t$=t2;
②当2<t≤4时,S=$\frac{1}{2}$×4t=2t;
③当4$<t≤\frac{16}{3}$时,S=-6t+32.
故选:A.
点评 本题主要考查的是动点问题的函数图象,根据题意求出函数的表达式是解题的关键.

练习册系列答案
相关题目
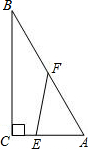 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点E是直角边AC上动点(点E与A、C两点均不重合),点F是斜边AB上的动点(点F与A、B两点均不重合).设AE长为x.
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点E是直角边AC上动点(点E与A、C两点均不重合),点F是斜边AB上的动点(点F与A、B两点均不重合).设AE长为x.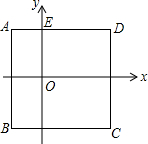 如图,已知正方形ABCD的边长为10,E(0,5),C(7,-5),一根细绳长155,从点E出发,顺时针绕在正方形上,将绳子的另一端到达的位置点F用坐标表示出来.
如图,已知正方形ABCD的边长为10,E(0,5),C(7,-5),一根细绳长155,从点E出发,顺时针绕在正方形上,将绳子的另一端到达的位置点F用坐标表示出来. 已知,如图,四边形ABCD的对角线AC与BD相交于点O,AD∥BC,求证:$\frac{OD}{OB}$=$\frac{OA}{OC}$.
已知,如图,四边形ABCD的对角线AC与BD相交于点O,AD∥BC,求证:$\frac{OD}{OB}$=$\frac{OA}{OC}$.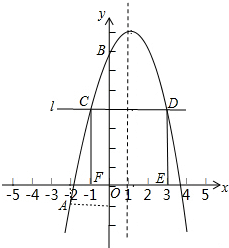 如图,已知二次函数y=-x2+bx+c的图象经过A(-2,-1),B(0,7)两点.
如图,已知二次函数y=-x2+bx+c的图象经过A(-2,-1),B(0,7)两点.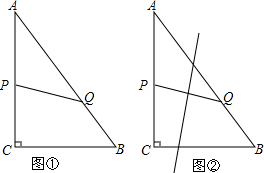
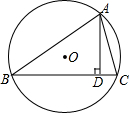 如图,O是△ABC的外心,AD是BC边上的高,R是△ABC外接圆的半径.问:
如图,O是△ABC的外心,AD是BC边上的高,R是△ABC外接圆的半径.问: