题目内容
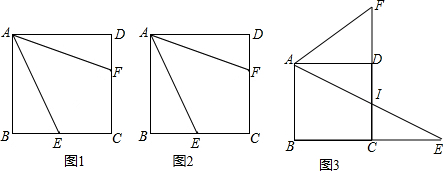
11.在正方形ABCD中,点E是射线BC上的点,直线AF与直线AB关于直线AE对称,直线AF交射线CD于点F.(1)当点E是线段BC的中点时,求证:AF=AB+CF.
(2)当∠BAE=30°时,求证:AF=2AB-2CF;
(3)当∠BAE=60°时,(2)中的结论是否还成立?若不成立,请判断AF与AB、CF之间的数量关系,并加以证明.
分析 (1)由折叠的性质得出AG=AB,BE=GE,进而用HL判断出Rt△EGF≌Rt△ECF,代换即可得出结论;
(2)利用含30°的直角三角形的性质即可;
(3)先判断出△AIF为等边三角形,得出AI=FI=AF,再代换即可得出结论.
解答 证明:如图1,
过点E作EG⊥AF与点G,连接EF.
由折叠知,△ABE≌△AGE,
∴AG=AB,BE=GE
∵BE=CE,
∴GE=CE,
∵在Rt△EGF和Rt△ECF中,$\left\{\begin{array}{l}{EF=EF}\\{EG=EC}\end{array}\right.$
∴Rt△EGF≌Rt△ECF,
∴FG=FC
∵AF=AG+FG
∴AF=AB+FC,
(2)如图2,
延长AF、BC交于点H.
由折叠知,∠BAE=∠HAE=30°,
∴∠H=30°
∴AH=2AB
同理:FH=2FC
∵AF=AH-FH
∴AF=2AB-2FC,
(3)由折叠知,∠BAE=∠HAE=60°,
∴∠DAE=∠DAF=30°,
∴△AIF为等边三角形
∴AF=AI=FI
由(2)可得AE=2AB
IE=2IC
∵IC=FC-FI
∴IC=FC-AF
∴IE=2FC-2AF
∵AI=AE-IE
∴AF=2AB-(2FC-2AF)
=2FC-2AB,
点评 此题是四边形综合题,主要考查了正方形的性质,折叠的性质,直角三角形的性质,等边三角形的性质,解本题的关键是找出线段之间的关系.

练习册系列答案
相关题目
1.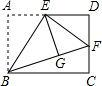 如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=$\sqrt{96}$,则DF的长为 ( )
如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=$\sqrt{96}$,则DF的长为 ( )
 如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=$\sqrt{96}$,则DF的长为 ( )
如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=$\sqrt{96}$,则DF的长为 ( )| A. | 2 | B. | 4 | C. | $\sqrt{6}$ | D. | $2\sqrt{3}$ |
2.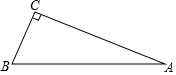 如图,在Rt△ABC中,∠C=90°,AB=13,AC=12,则∠A的正弦值为( )
如图,在Rt△ABC中,∠C=90°,AB=13,AC=12,则∠A的正弦值为( )
 如图,在Rt△ABC中,∠C=90°,AB=13,AC=12,则∠A的正弦值为( )
如图,在Rt△ABC中,∠C=90°,AB=13,AC=12,则∠A的正弦值为( )| A. | $\frac{5}{12}$ | B. | $\frac{12}{13}$ | C. | $\frac{12}{5}$ | D. | $\frac{5}{13}$ |
1.下列结论中,正确的是( )
| A. | 单项式$\frac{3πx{y}^{2}}{7}$的系数是$\frac{3}{7}$,次数是4 | |
| B. | 单项式m的次数是1,没有系数 | |
| C. | 单项式-xy2z的系数是-1,次数是4 | |
| D. | 多项式2x2+xy+3是四次三项式 |

 如图:函数y1=$\frac{1}{2}$x-2和y=-3x+5交于点A(2,-1),当x<2 时y1<y2.
如图:函数y1=$\frac{1}{2}$x-2和y=-3x+5交于点A(2,-1),当x<2 时y1<y2.