题目内容
19.阅读材料:如果一个矩形的宽与长的比值恰好为黄金比,人们就称它为“黄金矩形”(Golden Rectangle).在很多艺术品以及大自然中都能找到它,希腊雅典的巴特农神庙、法国巴黎圣母院就是很好的例子.
小明想画出一个黄金矩形,经过思考,他决定先画一个边长为2的正方形ABCD,如图1,取CD边的中点E,连接BE,在BE上截取EF=EC,在BC上截取BG=BF;然后,小明作了两条互相垂直的射线,如图2,OF⊥OG于点O.小明利用图1中的线段,在图2中作出一个黄金矩形OMPN,且点M在射线OF上,点N在射线OG上.
请你帮助小明在图1中完成作图,要求尺规作图,保留作图痕迹.
(1)求CG的长;
(2)图1中哪两条线段的比是黄金比?请你指出其中一组线段;
(3)请你利用(2)中的结论,在图2中作出一个黄金矩形OMPN,且点M在射线OF上,点N在射线OG上.要求尺规作图,保留作图痕迹.
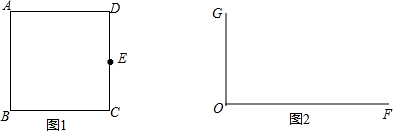
分析 利用题目提示直接画出图形,
(1)先利用勾股定理求出BE,再用作图即可求出CG,
(2)求出CG:BG,即可得出结论,判断出结论;
(3)借助小明的作出的线段,再借助线段的长度,即可作出图形.
解答 解:补全小明的图形如图1所示,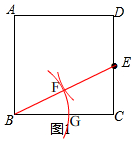
(1)∵正方形的边长为2,
∴BC=CD=2,
∵点E是CD中点,
∴CE=$\frac{1}{2}$CD=1,
在Rt△BCE中,BE=$\sqrt{B{C}^{2}+C{E}^{2}}$=$\sqrt{5}$,
由作图知,EF=CE=1,
∴BF=BE-EF=$\sqrt{5}$-1,
由作图知,BG=BF=$\sqrt{5}$-1,
∴CG=BC-BG=3-$\sqrt{5}$,
(2)由(1)知,BG=$\sqrt{5}$-1,CG=3-$\sqrt{5}$,
∴$\frac{CG}{BG}=\frac{3-\sqrt{5}}{\sqrt{5-1}}$=$\frac{\sqrt{5}-1}{2}$,
∴CG,BG的比是黄金比;
(3)如图2所示,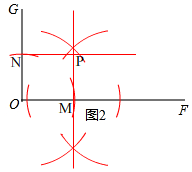
点评 此题是四边形综合题,主要考查了基本作图,勾股定理,线段的比,解本题的关键是掌握几种基本作图,是一道比较简单的综合题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
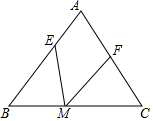 在△ABC中,AB=AC,BE=CM,BM=CF,∠EMF=50°,则∠A=80度.
在△ABC中,AB=AC,BE=CM,BM=CF,∠EMF=50°,则∠A=80度.
 在平面直角坐标系xOy中,抛物线y=-x2+mx+n与x轴交于点A,B(A在B的左侧).
在平面直角坐标系xOy中,抛物线y=-x2+mx+n与x轴交于点A,B(A在B的左侧).