题目内容
13. 如图,把一张矩形纸片ABCD沿对角线DB折叠,DE交AB于F,连AE.若∠DBC=58°,则∠AEF=32°.
如图,把一张矩形纸片ABCD沿对角线DB折叠,DE交AB于F,连AE.若∠DBC=58°,则∠AEF=32°.
分析 先根据全等三角形的性质,得出∠AEF=∠EAB,∠ABD=∠EDB,再根据∠AFE=∠DFB,可得∠AEF=∠BDE,最后根据Rt△BCD中,∠DBC=58°,得出∠BDC=32°,即∠BDE=32°,进而得出∠AEF=32°.
解答  解:∵矩形纸片ABCD沿对角线DB折叠,
解:∵矩形纸片ABCD沿对角线DB折叠,
∴BE=DA,DE=BA,
又∵AE=EA,
∴△AED≌△EAB,
∴∠AEF=∠EAB,
同理可得,△ABD≌△EDB,
∴∠ABD=∠EDB,
又∵∠AFE=∠DFB,
∴∠AEF=∠BDE,
∵Rt△BCD中,∠DBC=58°,
∴∠BDC=32°,
∴∠BDE=32°,
∴∠AEF=32°,
故答案为:32°
点评 本题主要考查了矩形的性质,以及平行线的性质,解题时注意:矩形的对边相等.

练习册系列答案
相关题目
18.小李有2根木棒,长度分别为10cm和15cm,要组成一个三角形(木棒的首尾分别相连接),还需在下列4根木棒中选取( )
| A. | 4cm长的木棒 | B. | 5cm长的木棒 | C. | 20cm长的木棒 | D. | 25cm长的木棒 |
3.a的平方的5倍减去3的差,应写成( )
| A. | 5a2-3 | B. | 5(a2-3) | C. | (5a)2-3 | D. | a2(5-3) |
 如图,在⊙O中,AB=AC,∠B=70°,则∠C=70°.
如图,在⊙O中,AB=AC,∠B=70°,则∠C=70°.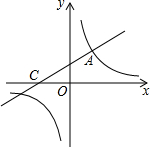 如图,直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$相交于点A(m,3),与x轴交于点C.
如图,直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$相交于点A(m,3),与x轴交于点C.