题目内容
17.若圆的半径是2cm,一条弦长是2$\sqrt{3}$,则圆心到该弦的距离是1cm,该弦所对的圆心角的度数为120°.分析 直接利用勾股定理以及垂径定理得出CO的长,再利用三角函数值求出答案.
解答  解:如图所示:过点O作OC⊥AB于点C,
解:如图所示:过点O作OC⊥AB于点C,
∵圆的半径是2cm,一条弦长是2$\sqrt{3}$,
∴AO=BO=2cm,AC=BC=$\sqrt{3}$cm,
∴CO=$\sqrt{A{O}^{2}-A{C}^{2}}$=1(cm),
∴sin∠COA=$\frac{AC}{AO}$=$\frac{\sqrt{3}}{2}$,
∴∠COA=60°,
∴∠BOA=120°.
故答案为:1cm,120°.
点评 此题主要考查了垂径定理以及勾股定理等知识,根据题意画出图形结合垂径定理得出CO的长是解题关键.

练习册系列答案
相关题目
5.下列一元二次方程中无实数解的是( )
| A. | x2+2x+1=0 | B. | x2=2x-1 | C. | x2+1=0 | D. | x2-4x-5=0 |
 如图,AC=BD,BC=AD,求证:∠C=∠D.
如图,AC=BD,BC=AD,求证:∠C=∠D. 如图,a、b为数轴上不同两点.则:
如图,a、b为数轴上不同两点.则: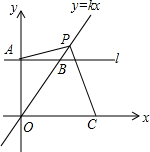 如图,直线l∥x轴,交y轴于点A(0,2),交直线y=kx于点B,P是线段OB延长线上一点,连接AP作PC⊥AP交x轴于点C,连接AC交OB于D,E是直线CP与y轴的交点.如果∠ACE=∠AEC,$\frac{PD}{OD}$=2,求$\frac{PA}{PC}$的值.
如图,直线l∥x轴,交y轴于点A(0,2),交直线y=kx于点B,P是线段OB延长线上一点,连接AP作PC⊥AP交x轴于点C,连接AC交OB于D,E是直线CP与y轴的交点.如果∠ACE=∠AEC,$\frac{PD}{OD}$=2,求$\frac{PA}{PC}$的值.