题目内容
9.a是不为1的有理数,我们把$\frac{1}{1-a}$称为1的差倒数,如-1的差倒数是$\frac{1}{1-(-1)}=\frac{1}{2}$.已知${a_1}=-\frac{1}{3}$,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数…,以此类推,a2012的差倒数a2013=-$\frac{1}{3}$.分析 计算出前面的几个数据即可发现规律,3个数一个轮回,于是a2013=a4
解答 解:由题意得,a1=-$\frac{1}{3}$,a2=$\frac{3}{4}$,a3=4,a4=-$\frac{1}{3}$,a5=$\frac{3}{4}$,a6=4
于是发现,2013是3的整数倍,
∴a2013=-$\frac{1}{3}$,
故答案为-$\frac{1}{3}$.
点评 熟练地找到这些数之间的规律是解题的关键.

练习册系列答案
相关题目
14.下列有理数的大小比较,正确的是( )
| A. | -5>0.1 | B. | 0>$\frac{1}{5}$ | C. | -5.1<-4.2 | D. | 0<$-\frac{1}{4}$ |
 如图,宽为30cm的长方形图案由10个全等的小长方形拼成,其中一个小长方形的长为24cm.
如图,宽为30cm的长方形图案由10个全等的小长方形拼成,其中一个小长方形的长为24cm.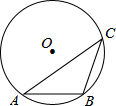 如图,在半径为5的⊙O中,弦AB=4,点C是优弧AB上一点(不与A、B重合),则sinC的值为$\frac{2}{5}$.
如图,在半径为5的⊙O中,弦AB=4,点C是优弧AB上一点(不与A、B重合),则sinC的值为$\frac{2}{5}$. 已知:线段a,∠α.
已知:线段a,∠α. 如图,若PE平分∠BEF,PF平分∠DFE,∠1=35°,∠2=55°,则AB与CD平行吗?为什么?
如图,若PE平分∠BEF,PF平分∠DFE,∠1=35°,∠2=55°,则AB与CD平行吗?为什么?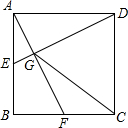 如图,点E、F分别为正方形ABCD中AB、BC边的中点,连接AF、DE相交于点G,连接CG,则tan∠CGD=2.
如图,点E、F分别为正方形ABCD中AB、BC边的中点,连接AF、DE相交于点G,连接CG,则tan∠CGD=2. 如图,∠ABC=90°,∠CBD=40°,则∠ABD的度数是50°.
如图,∠ABC=90°,∠CBD=40°,则∠ABD的度数是50°.