题目内容
18.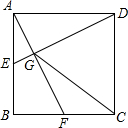 如图,点E、F分别为正方形ABCD中AB、BC边的中点,连接AF、DE相交于点G,连接CG,则tan∠CGD=2.
如图,点E、F分别为正方形ABCD中AB、BC边的中点,连接AF、DE相交于点G,连接CG,则tan∠CGD=2.
分析 证明△ABF≌△DAE,得∠AED=∠BFA,证出AF⊥DE,取AD的中点H,连接CH,证明MH是三角形ADG的中位线,证出CH垂直平分DG,证出∠CGD=∠AED,即可得出tan∠CGD=tan∠AED.
解答 解:如图所示:在正方形ABCD中,AB=AD,∠B=∠BAD=90°,
∵E、F分别为AB、BC边的中点,
∴AE=BF,
在△ABF和△DAE中,$\left\{\begin{array}{l}{AB=AD}&{\;}\\{∠B=∠BAD=90°}&{\;}\\{AE=BF}&{\;}\end{array}\right.$,
∴△ABF≌△DAE(SAS),
∴∠AED=∠BFA,
∵∠BAF+∠AED=∠BAF+∠BFA=90°,
∴∠AGE=90°,
∴AF⊥DE,
取AD的中点H,连接CH,
∵H是AD的中点,CH∥AF,
设CH与DG相交于点M,则MH是三角形ADG的中位线,
∴DM=GM,
∴CH垂直平分DG,
∴CD=CG,
∴∠CGD=∠CDG,
∵AB∥CD,
∴∠CGD=∠AED,
设正方形的边长为2a,则AE=a,tan∠CGD=tan∠AED=$\frac{2a}{a}$=2;
故答案为:2.
点评 本题考查了正方形的性质、等腰三角形的判定、等腰三角形的判定与性质、锐角三角函数的运用;本题有一定难度,需要通过作辅助线才能得出结果.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 按下图解答以下问题
按下图解答以下问题
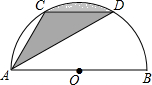 如图,C,D是以AB为直径的半圆周上的两点,且AB=8cm,弧$\widehat{CD}$的度数为60°,线段AC,AD与弧CD围成了图中的阴影部分.
如图,C,D是以AB为直径的半圆周上的两点,且AB=8cm,弧$\widehat{CD}$的度数为60°,线段AC,AD与弧CD围成了图中的阴影部分.


