题目内容
4.在平面直角坐标系中,一次函数y=kx+b的图象与x轴、y轴分别相交于点A(-3,0)、B(0,-3)两点,二次函数y=x2+mx+n的图象经过点A.(1)求一次函数y=kx+b的表达式;
(2)若二次函数y=x2+mx+n图象的顶点在直线AB上,求m,n;
(3)①?设m=-2,当-3≤x≤0时,求二次函数y=x2+mx+n的最小值;
?②若当-3≤x≤0时,二次函数y=x2+mx+n的最小值为-4,求m,n的值.
分析 (1)利用待定系数法求出解析式,
(2)先表示出二次函数y=x2+mx+n图象的顶点,利用直线AB列出式子,再与点A在二次函数上得到的式子组成方程组求得m,n的值,
(3)①易求抛物线解析式为y=x2-2x-15.根据抛物线的对称性和增减性来求二次函数y=x2+mx+n的最小值;
②本题要分四种情况:当对称轴-3<-$\frac{m}{2}$<0时;当对称轴-$\frac{m}{2}$>0时;当对称轴-$\frac{m}{2}$=0时;当对称轴-$\frac{m}{2}$≤-3时,结合二次函数y=x2+mx+n的图象经过点A得出式子9-3m+n=0,求出m,n但一定要验证是否符合题意.
解答 解:(1)A(-3,0),B(0,-3)代入y=kx+b得
$\left\{\begin{array}{l}{0=-3k+b}\\{-3=b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=-3}\end{array}\right.$.
∴一次函数y=kx+b的解析式为:y=-x-3;
(2)二次函数y=x2+mx+n图象的顶点为(-$\frac{m}{2}$,$\frac{4n-{m}^{2}}{4}$)
∵顶点在直线AB上,
∴$\frac{4n-{m}^{2}}{4}$=$\frac{m}{2}$-3,
又∵二次函数y=x2+mx+n的图象经过点A(-3,0),
∴9-3m+n=0,
∴组成方程组为$\left\{\begin{array}{l}{\frac{4n-{m}^{2}}{4}=\frac{m}{2}-3}\\{9-3m+n=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=4}\\{n=3}\end{array}\right.$或$\left\{\begin{array}{l}{m=6}\\{n=9}\end{array}\right.$.
(3)①当m=-2时,9-3m+n=0,
解得 n=-15,
∴y=x2-2x-15.
∵对称轴直线x=1在-3≤x≤0右侧,
∴x=0时,y最小值是-15.
∵二次函数y=x2+mx+n的图象经过点A.
∴9-3m+n=0,
∴当-3≤x≤0时,二次函数y=x2+mx+n的最小值为-4;
②如图1,i)当对称轴-3<-$\frac{m}{2}$<0时,最小值为$\frac{4n-{m}^{2}}{4}$=-4,与9-3m+n=0,组成方程组为$\left\{\begin{array}{l}{\frac{4n-{m}^{2}}{4}=-4}\\{9-3m+n=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=2}\\{n=-3}\end{array}\right.$或$\left\{\begin{array}{l}{m=10}\\{n=21}\end{array}\right.$(由-3<-$\frac{m}{2}$<0知不符合题意舍去)
所以$\left\{\begin{array}{l}{m=2}\\{n=-3}\end{array}\right.$.
ii)如图2,当对称轴-$\frac{m}{2}$>0时,在-3≤x≤0时,x为0时有最小值为-4, 把(0,-4)代入y=x2+mx+n得n=-4,
把(0,-4)代入y=x2+mx+n得n=-4,
把n=-4代入9-3m+n=0,得m=$\frac{5}{3}$.
∵-$\frac{m}{2}$>0,
∴m<-2,
∴此种情况不成立,
iii)当对称轴-$\frac{m}{2}$=0时,y=x2+mx+n的最小值为-4,
把(0,-4)代入y=x2+mx+n得n=-4,
把n=-4代入9-3m+n=0,得m=$\frac{5}{3}$.
∵-$\frac{m}{2}$=0,
∴m=0,
∴此种情况不成立,
iiii)当对称轴-$\frac{m}{2}$≤-3时,最小值为0,不成立.
综上所述,m=2,n=-3.
点评 本题主要考查了二次函数综合题,解题的关键是在讨论对称轴不同位置得出m,n的值时,要结合对称轴看结果是否符合题意.

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案| 自来水销售价格 | 污水处理价格 | |
| 每户每月用水量 | 单价:元/吨 | 单价:元/吨 |
| 20吨以下(含20吨) | a | 1.50 |
| 超过20吨但不超过30吨的部分 | b | 1.50 |
| 超过30吨的部分 | 4.50 | 1.50 |
已知小王家2012年4月份用水22吨,交水费80元;5月份用水25吨,交水费95元.
(1)求a,b的值;
(2)随着夏天的到来,用水量将增加.为了节省开支,小王计划把6月份的水费控制在不超过181元,则小王家6月份最多能用水多少吨(结果保留整数)?
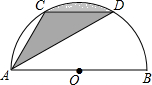 如图,C,D是以AB为直径的半圆周上的两点,且AB=8cm,弧$\widehat{CD}$的度数为60°,线段AC,AD与弧CD围成了图中的阴影部分.
如图,C,D是以AB为直径的半圆周上的两点,且AB=8cm,弧$\widehat{CD}$的度数为60°,线段AC,AD与弧CD围成了图中的阴影部分.