题目内容
9.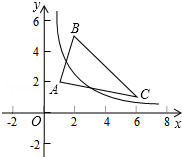 如图,△ABC的三个顶点分别为A(1,2),B(2,5),C(6,1).若函数y=$\frac{k}{x}$在第一象限内的图象与△ABC有交点,则k的取值范围是2≤k≤$\frac{49}{4}$.
如图,△ABC的三个顶点分别为A(1,2),B(2,5),C(6,1).若函数y=$\frac{k}{x}$在第一象限内的图象与△ABC有交点,则k的取值范围是2≤k≤$\frac{49}{4}$.
分析 根据反比例函数图象上点的坐标特征,反比例函数和三角形有交点的临界条件分别是交点为A、与线段BC有交点,由此求解即可.
解答 解:反比例函数和三角形有交点的第一个临界点是交点为A,
∵过点A(1,2)的反比例函数解析式为y=$\frac{2}{x}$,
∴k≥2.
随着k值的增大,反比例函数的图象必须和线段BC有交点才能满足题意,
经过B(2,5),C(6,1)的直线解析式为y=-x+7,
$\left\{\begin{array}{l}{y=-x+7}\\{y=\frac{k}{x}}\end{array}\right.$,得x2-7x+k=0
根据△≥0,得k≤$\frac{49}{4}$,
综上可知2≤k≤$\frac{49}{4}$.
故答案为2≤k≤$\frac{49}{4}$.
点评 本题考查了反比例函数图象上点的坐标特征,两函数交点坐标的求法,有一定难度.注意自变量的取值范围.

练习册系列答案
相关题目
1. 如图是一块电脑主板的示意图,每一转角处都是直角,数据如图所示(单位:mm),则该主板的周长是( )
如图是一块电脑主板的示意图,每一转角处都是直角,数据如图所示(单位:mm),则该主板的周长是( )
 如图是一块电脑主板的示意图,每一转角处都是直角,数据如图所示(单位:mm),则该主板的周长是( )
如图是一块电脑主板的示意图,每一转角处都是直角,数据如图所示(单位:mm),则该主板的周长是( )| A. | 88mm | B. | 96mm | C. | 80mm | D. | 84mm |
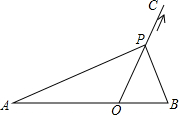 如图,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动.设运动时间为t秒,当△ABP是直角三角形时,t的值为1或$\frac{-1+\sqrt{33}}{8}$.
如图,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动.设运动时间为t秒,当△ABP是直角三角形时,t的值为1或$\frac{-1+\sqrt{33}}{8}$.

 如图,BE、CF都是△ABC的角平分线,且∠BDC=110°,则∠A=40°.
如图,BE、CF都是△ABC的角平分线,且∠BDC=110°,则∠A=40°.