题目内容
用指定的方法解下列方程:
①x2+2x-35=0(配方法解)
②4x2-3=12x(用公式法解)
①x2+2x-35=0(配方法解)
②4x2-3=12x(用公式法解)
考点:解一元二次方程-公式法,解一元二次方程-配方法
专题:
分析:(1)根据配方法,可得方程的解;
(2)根据公式法,可得方程的解.
(2)根据公式法,可得方程的解.
解答:解:①移项,得
x2+2x=35.
配方,得
2+2x+1=36,
即(x+1)2=36.
开方,得
x+1=±6,
x=15,x2=-7;
②移项,得
4x2-12x-3=0.
a=4,b=-12,c=-3,
△=b2-4ac=(-12)2-4×4×(-3)=192>0,
4x2-3=12x有不相等的二实根.
x1=
=
=
,
x2=
=
=
.
x2+2x=35.
配方,得
2+2x+1=36,
即(x+1)2=36.
开方,得
x+1=±6,
x=15,x2=-7;
②移项,得
4x2-12x-3=0.
a=4,b=-12,c=-3,
△=b2-4ac=(-12)2-4×4×(-3)=192>0,
4x2-3=12x有不相等的二实根.
x1=
-b+
| ||
| 2a |
-(-12)+
| ||
| 2×4 |
3+2
| ||
| 2 |
x2=
-b-
| ||
| 2a |
-(-12)-
| ||
| 2×4 |
3-2
| ||
| 2 |
点评:本题考查了解一元二次方程,公式法解一元二次方程先化成一般式,确定a、b、c的值,再用公式.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
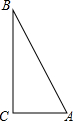 如图,△ABC是直角三角形,∠ACB=90°,在△ABC内剪出一块半圆,使圆心在BC边上,且半圆的弧与边AB相切.
如图,△ABC是直角三角形,∠ACB=90°,在△ABC内剪出一块半圆,使圆心在BC边上,且半圆的弧与边AB相切.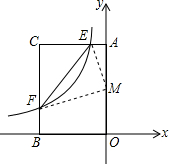 如图,在平面直角坐标系xOy中,矩形AOBC的AO边在y轴上,BO边在x轴上,C点坐标为(-2,3),反比例函数y=
如图,在平面直角坐标系xOy中,矩形AOBC的AO边在y轴上,BO边在x轴上,C点坐标为(-2,3),反比例函数y= 如图,△ABC中,∠C=90°,BC=5,O为△ABC的内心,若OC=
如图,△ABC中,∠C=90°,BC=5,O为△ABC的内心,若OC= 如图,已知,AC⊥BA,BD⊥CD,AC=BD,求证:∠ABO=∠DCO.
如图,已知,AC⊥BA,BD⊥CD,AC=BD,求证:∠ABO=∠DCO.