题目内容
半径为
的⊙O中,弦AB=2,弦AC=
,则BC= .
| 2 |
| 6 |
考点:圆周角定理,勾股定理
专题:分类讨论
分析:首先根据勾股定理及余弦定理分别求出∠AOB、∠AOC的大小,然后再次利用余弦定理即可求出BC的长.
解答: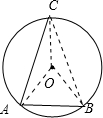 解:如图,连接OA、OB、OC、BC;
解:如图,连接OA、OB、OC、BC;
∵OA=OB=
,AB=2,
∴OA2+OB2=AB2,
∴△OAB为直角三角形,
∴∠AOB=90°;
又∵cos∠AOC=
=
=
=-
,
∴∠AOC=120°;
∴∠BOC=360°-90°-120°
=150°;
∴BC=
=
=
=
+1.
故答案为:
+1.
 解:如图,连接OA、OB、OC、BC;
解:如图,连接OA、OB、OC、BC;∵OA=OB=
| 2 |
∴OA2+OB2=AB2,
∴△OAB为直角三角形,
∴∠AOB=90°;
又∵cos∠AOC=
| OC2+OA2-AC2 |
| 2OA•OC |
=
2+2-(
| ||||
2×
|
=
| 4-6 |
| 4 |
=-
| 1 |
| 2 |
∴∠AOC=120°;
∴∠BOC=360°-90°-120°
=150°;
∴BC=
| OB2+OC2-2OB•OC•cos150° |
=
2+2-2×(
|
=
4+2
|
=
| 3 |
故答案为:
| 3 |
点评:该命题主要考查了勾股定理及其应用问题;解题的关键是根据题意结合图形,灵活运用勾股定理和余弦定理来分析、判断、求解或证明.

练习册系列答案
相关题目
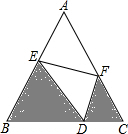 如图,已知D为BC上一点,∠B=∠C=∠EDF=60°,BE=6,CD=3,CF=4,求AF的长.
如图,已知D为BC上一点,∠B=∠C=∠EDF=60°,BE=6,CD=3,CF=4,求AF的长. 利用网格线作图:
利用网格线作图: 如图,正方形纸片ABCD的面积为1,点M、N分别在AD、BC上,且AM=BN=
如图,正方形纸片ABCD的面积为1,点M、N分别在AD、BC上,且AM=BN=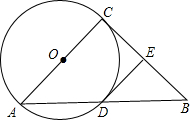 如图,以Rt△ABC的直角边AC为直径作⊙O,交AB于D,E为BC中点,求证:DE是⊙O的切线.
如图,以Rt△ABC的直角边AC为直径作⊙O,交AB于D,E为BC中点,求证:DE是⊙O的切线. 在正方形ABCD中,E是AB的中点,AF=
在正方形ABCD中,E是AB的中点,AF=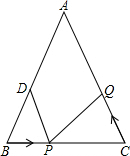 如图,在△ABC中,∠B=∠C,AB=10cm,点D为AB的中点.点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
如图,在△ABC中,∠B=∠C,AB=10cm,点D为AB的中点.点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.