题目内容
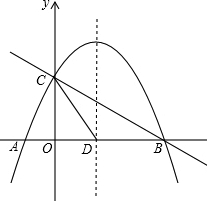 如图,抛物线y=-
如图,抛物线y=-| 4 |
| 7 |
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
考点:二次函数综合题
专题:压轴题
分析:(1)把点A、C的坐标代入函数解析式,利用待定系数法求二次函数解析式解答即可;
(2)根据抛物线解析式求出点D的坐标,再利用勾股定理列式求出CD,然后分点P在x轴上方和下方两种情况写出点P的坐标即可;
(3)求出点B的坐标,然后根据△BCD的面积不变确定出△BCF的面积最大时四边形CDBF的面积最大,利用待定系数法求一次函数解析式求出直线BC的解析式,然后表示出EF,利用三角形的面积公式求出△BCF的面积,再利用二次函数的最值问题求出△BCF的面积和点E的横坐标,然后求解即可.
(2)根据抛物线解析式求出点D的坐标,再利用勾股定理列式求出CD,然后分点P在x轴上方和下方两种情况写出点P的坐标即可;
(3)求出点B的坐标,然后根据△BCD的面积不变确定出△BCF的面积最大时四边形CDBF的面积最大,利用待定系数法求一次函数解析式求出直线BC的解析式,然后表示出EF,利用三角形的面积公式求出△BCF的面积,再利用二次函数的最值问题求出△BCF的面积和点E的横坐标,然后求解即可.
解答:解:(1)将点A(-1,0),C(0,4)代入抛物线得
,
解得
.
所以,抛物线解析式为y=-
x2+
x+4;
(2)∵y=-
x2+
x+4=-
(x-3)2+
,
∴点D的坐标为(3,0),
由勾股定理得,CD=
=
=5,
∵△PCD是以CD为腰的等腰三角形,
∴点P在x轴上方时,坐标为(3,8),
点P在x轴下方时,坐标为(3,-5);
(3)令y=0,则-
x2+
x+4=0,
整理得,x2-6x-7=0,
解得x1=-1,x2=7,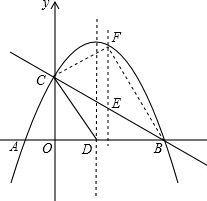
所以,点B的坐标为(7,0),
∵△BCD的面积不变,
∴△BCF的面积最大时四边形CDBF的面积最大,
S△BCD=
×(7-3)×4=8,
设直线BC的解析式为y=kx+b,
则
,
解得
,
所以,y=-
x+4,
则EF=(-
x2+
x+4)-(-
x+4)=-
x2+4x,
所以,S△BCF=
(-
x2+4x)×7=-2x2+14x=-2(x-
)2+
,
∵-2<0,
∴当x=
时,S△BCF有最大值
,
此时,y=-
×
+4=-2+4=2,
所以,点E运动到(
,2)时,四边形CDBF的面积最大,
最大值=S△BCD+S△BCF=8+
=
.
|
解得
|
所以,抛物线解析式为y=-
| 4 |
| 7 |
| 24 |
| 7 |
(2)∵y=-
| 4 |
| 7 |
| 24 |
| 7 |
| 4 |
| 7 |
| 64 |
| 7 |
∴点D的坐标为(3,0),
由勾股定理得,CD=
| OC2+OD2 |
| 42+32 |
∵△PCD是以CD为腰的等腰三角形,
∴点P在x轴上方时,坐标为(3,8),
点P在x轴下方时,坐标为(3,-5);
(3)令y=0,则-
| 4 |
| 7 |
| 24 |
| 7 |
整理得,x2-6x-7=0,
解得x1=-1,x2=7,

所以,点B的坐标为(7,0),
∵△BCD的面积不变,
∴△BCF的面积最大时四边形CDBF的面积最大,
S△BCD=
| 1 |
| 2 |
设直线BC的解析式为y=kx+b,
则
|
解得
|
所以,y=-
| 4 |
| 7 |
则EF=(-
| 4 |
| 7 |
| 24 |
| 7 |
| 4 |
| 7 |
| 4 |
| 7 |
所以,S△BCF=
| 1 |
| 2 |
| 4 |
| 7 |
| 7 |
| 2 |
| 49 |
| 2 |
∵-2<0,
∴当x=
| 7 |
| 2 |
| 49 |
| 2 |
此时,y=-
| 4 |
| 7 |
| 7 |
| 2 |
所以,点E运动到(
| 7 |
| 2 |
最大值=S△BCD+S△BCF=8+
| 49 |
| 2 |
| 65 |
| 2 |
点评:本题是二次函数综合题型,主要利用了待定系数法求二次函数解析式,待定系数法求一次函数解析式,勾股定理.三角形的面积,难点在于(2)分情况讨论,(3)判断出△BCF的面积最大时四边形CDBF的面积最大并表示出△BCF的面积.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
一种商品,降价20%后的售价是a元,则原价为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
A和B都是6次多项式,则A+B一定是( )
| A、6次多项式 |
| B、12次多项式 |
| C、次数不低于6的多项式 |
| D、次数不高于6的多项式或单项式 |
 小雨的爸爸从市场买回来四个大西瓜,爸爸为了考一考小雨,让小雨把四个大西瓜依次边上①,②,③,④号后,按质量由小到大的顺序排列出来(不准用称),小雨用一个简易天平操作,操作如下:(操作过程中,天平自身损坏忽略不计)
小雨的爸爸从市场买回来四个大西瓜,爸爸为了考一考小雨,让小雨把四个大西瓜依次边上①,②,③,④号后,按质量由小到大的顺序排列出来(不准用称),小雨用一个简易天平操作,操作如下:(操作过程中,天平自身损坏忽略不计)