题目内容
18.某县教师进修学校初中研训部欲招聘一名打字员,对甲、乙两位候选人分别进行了工作态度、操作技能和学科知识的考核,他们的成绩如表所示(单位:分):(1)若该初中研训部认为工作态度、操作技能和学科知识同等重要,则谁将被聘用?
| 候选人 | 工作态度 | 操作技能 | 学科知识 |
| 甲 | 83 | 79 | 81 |
| 乙 | 74 | 83 | 82 |
分析 (1)根据算术平均数的计算方法,分别求出两人的平均成绩各是多少;然后比较大小,判断出谁将被聘用即可.
(2)根据加权平均数的计算方法,分别求出两人的平均成绩各是多少;然后比较大小,判断出谁将被聘用即可.
解答 解:(1)$\overline{甲}$=(83+79+81)÷3=243÷3=81(分),
$\overline{乙}$=(74+83+82)÷3=239÷3≈79.7(分),
∵81>79.7,
∴甲将被聘用.
(2)$\overline{甲}$=(83×2+79×5+81×3)÷(2+5+3)=804÷10=80.4(分),
$\overline{乙}$=(74×2+83×5+82×3)÷(2+5+3)=809÷10=80.9(分),
∵80.9>80.4,
∴乙将被聘用.
点评 (1)此题主要考查了算术平均数的含义和求法,要熟练掌握,解答此题的关键是要明确:平均数是指在一组数据中所有数据之和再除以数据的个数.它是反映数据集中趋势的一项指标.
(2)此题还考查了加权平均数的含义和求法,要熟练掌握,解答此题的关键是要明确:数据的权能够反映数据的相对“重要程度”,要突出某个数据,只需要给它较大的“权”,权的差异对结果会产生直接的影响.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.一辆加满汽油的汽车在匀速行驶中,油箱中的剩余油量Q(1)与行驶的时间t(h)的关系如下表所示:
请你根据表格,解答下列问题:
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)随着行驶的时间的不断增加,油箱中的剩余油量的变化趋势是怎样的?
(3)请直接写出Q与t的关系式,并求出这辆汽车在连续行驶6h后,油箱中的剩余油量;
(4)这辆车在中途不加油的情况下,最多能连续行驶的时间是多少?
| 行驶时间t(h) | 0 | 1 | 2 | 3 | 4 | … |
| 油箱中的剩余油量Q(1) | 54 | 46.5 | 39 | 31.5 | 24 | … |
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)随着行驶的时间的不断增加,油箱中的剩余油量的变化趋势是怎样的?
(3)请直接写出Q与t的关系式,并求出这辆汽车在连续行驶6h后,油箱中的剩余油量;
(4)这辆车在中途不加油的情况下,最多能连续行驶的时间是多少?
13.在?ABCD中,AB=3,AD=5,则?ABCD的周长为( )
| A. | 8 | B. | 10 | C. | 12 | D. | 16 |
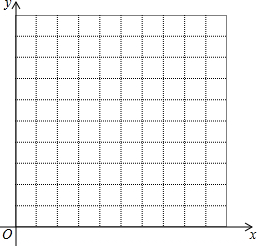 在平面直角坐标系中,点P从原点O出发,且点P只能每次向上平移2个单位长度或向右平移1个单位长度.
在平面直角坐标系中,点P从原点O出发,且点P只能每次向上平移2个单位长度或向右平移1个单位长度.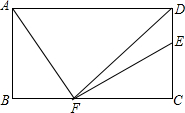 如图,矩形ABCD中,AD=12,AB=7,DF平分∠ADC,AF⊥EF.
如图,矩形ABCD中,AD=12,AB=7,DF平分∠ADC,AF⊥EF.