Question

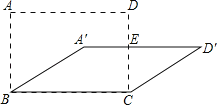
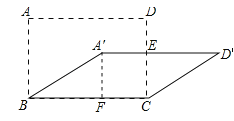
【题目】如图，若将四根木条钉成的矩形木框ABCD变形为平行四边形A′BCD′，并使其面积为矩形ABCD面积的一半，若A′D′与CD交于点E，且AB＝2，则△ECD′的面积是_____．

Answer 1

【答案】

【解析】

作A'F⊥BC于F，则∠A'FB＝90°，根据题意得：平行四边形A′BCD′的面积＝BCA'F＝BCAB， A'F＝AB＝1，得出∠D＝∠B＝30°，得出BF＝A'F＝，由矩形和平行四边形的性质得出BC＝AD＝A'D'，A'D'∥AD∥BC，CD⊥BC，得出CD⊥A'D'，得出A'F∥CD，证出四边形A'ECF是矩形，得出CE＝A'F＝1，A'E＝CF，证出D’E＝BF＝，即可得出答案．

解：作A'F⊥BC于F，如图所示：

则∠A'FB＝90°，

根据题意得：平行四边形A′BCD′的面积＝BCA'F＝BCAB，

∴A'F＝AB＝1，

∴∠D＝∠B＝30°，

∴BF＝A'F＝，

∵四边形ABCD是矩形，四边形A′BCD′是平行四边形，

∴BC＝AD＝A'D'，A'D'∥AD∥BC，CD⊥BC，

∴CD⊥A'D'，

∴A'F∥CD，

∴四边形A'ECF是矩形，

∴CE＝A'F＝1，A'E＝CF，

∴D’E＝BF＝，

∴△ECD’的面积＝DE×CE＝××1＝；

故答案为：．