Question

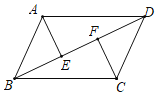
【题目】如图，BD是ABCD的对角线，点E、F分别在BD上，连接AE、CF．

（1）请你添加一个条件，使△AED≌△CFB，并给予证明；

（2）在你添加的条件后，不再添加其它条件，写出图中所有全等的三角形．

Answer 1

【答案】（1）DE＝BF，见解析；（2）△AED≌△CFB，△ABD≌△CDB，△ABE≌△CDF，见解析

【解析】

（1）添加条件：DE＝BF；由平行四边形的性质得出AD＝BC，AD∥BC，∴∠ADE＝∠CBF，由SAS证明△AED≌△CFB即可；

（2）由（1）得：△AED≌△CFB；得出AE＝CF，由SSS证明△ABD≌△CDB，由SSS证明△ABE≌△CDF即可．

解：（1）添加条件：DE＝BF；理由如下：

∵四边形ABCD是平行四边形，

∴AD＝BC，AD∥BC，

∴∠ADE＝∠CBF，

在△AED和△CFB中，，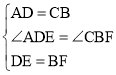

∴△AED≌△CFB（SAS）；

（2）图中所有全等的三角形为△AED≌△CFB，△ABD≌△CDB，△ABE≌△CDF；理由如下：

由（1）得：△AED≌△CFB；

∴AE＝CF，

∵四边形ABCD是平行四边形，

∴AD＝CB，AB＝CD，

在△ABD和△CDB中，，

∴△ABD≌△CDB（SSS）；

∵BF＝DE，

∴BE＝DF，

在△ABE和△CDF中，，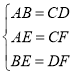

∴△ABE≌△CDF（SSS）．