题目内容
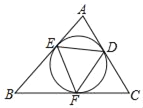
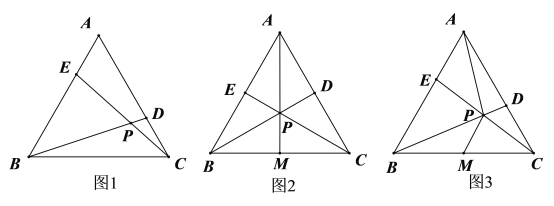
【题目】如图,在等边![]() 中,点
中,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的动点,且
上的动点,且![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
(1)如图1,求证![]() ;
;
(2)点![]() 是边
是边![]() 的中点,连接
的中点,连接![]() ,
,![]() .
.
①如图2,若点![]() ,
,![]() ,
,![]() 三点共线,则
三点共线,则![]() 与
与![]() 的数量关系是 ;
的数量关系是 ;
②若点![]() ,
,![]() ,
,![]() 三点不共线,如图3,问①中的结论还成立吗?若成立,请给出证明,若不成立,请说明理由.
三点不共线,如图3,问①中的结论还成立吗?若成立,请给出证明,若不成立,请说明理由.
【答案】(1)证明过程见详解;(2)①![]() ;②结论成立,证明见详解
;②结论成立,证明见详解
【解析】
(1)先证明![]() ,得出对应角相等,然后利用四边形的内角和和对顶角相等即可得出结论;
,得出对应角相等,然后利用四边形的内角和和对顶角相等即可得出结论;
(2)①![]() ;由等边三角形的性质和已知条件得出AM⊥BC,∠CAP=30°,可得PB=PC,由∠BPC=120°和等腰三角形的性质可得∠PCB=30°,进而可得AP=PC,由30°角的直角三角形的性质可得PC=2PM,于是可得结论;
;由等边三角形的性质和已知条件得出AM⊥BC,∠CAP=30°,可得PB=PC,由∠BPC=120°和等腰三角形的性质可得∠PCB=30°,进而可得AP=PC,由30°角的直角三角形的性质可得PC=2PM,于是可得结论;
②延长BP至D,使PD=PC,连接AD、CD,根据SAS可证△ACD≌△BCP,得出AD=BP,∠ADC=∠BPC=120°,然后延长PM至N,使MN=MP,连接CN,易证△CMN≌△BMP(SAS),可得CN=BP=AD,∠NCM=∠PBM,最后再根据SAS证明△ADP≌△NCP,即可证得结论.
(1)证明:因为△ABC为等边三角形,所以![]()
∵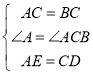 ,∴
,∴![]() ,∴
,∴![]() ,
,
在四边形AEPD中,∵![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ;
;
(2)①如图2,∵△ABC是等边三角形,点M是边BC的中点,
∴∠BAC=∠ABC=∠ACB=60°,AM⊥BC,∠CAP=![]() ∠BAC=30°,∴PB=PC,
∠BAC=30°,∴PB=PC,
∵∠BPC=120°,∴∠PBC=∠PCB=30°,
∴PC=2PM,∠ACP=60°﹣30°=30°=∠CAP,
∴AP=PC,∴AP=2PM;
故答案为:![]() ;
;
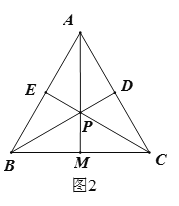
②AP=2PM成立,理由如下:
延长BP至D,使PD=PC,连接AD、CD,如图4所示:则∠CPD=180°﹣∠BPC=60°,
∴△PCD是等边三角形,
∴CD=PD=PC,∠PDC=∠PCD=60°,
∵△ABC是等边三角形,∴BC=AC,∠ACB=60°=∠PCD,
∴∠BCP=∠ACD,
∴△ACD≌△BCP(SAS),
∴AD=BP,∠ADC=∠BPC=120°,
∴∠ADP=120°﹣60°=60°,
延长PM至N,使MN=MP,连接CN,
∵点M是边BC的中点,∴CM=BM,
∴△CMN≌△BMP(SAS),
∴CN=BP=AD,∠NCM=∠PBM,
∴CN∥BP,∴∠NCP+∠BPC=180°,
∴∠NCP=60°=∠ADP,
在△ADP和△NCP中,∵AD=NC,∠ADP=∠NCP,PD=PC,
∴△ADP≌△NCP(SAS),
∴AP=PN=2CM;

【题目】某校为了了解学生对语文、数学、英语、物理四科的喜爱程度(每人只选一科),特对八年级某班进行了调查,并绘制成如下频数和频率统计表和扇形统计图:
科目 | 频数 | 频率 |
语文 |
| 0.5 |
数学 | 12 |
|
英语 | 6 |
|
物理 |
| 0.2 |
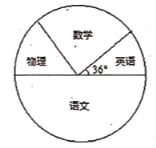
(1)求出这次调查的总人数;
(2)求出表中![]() 的值;
的值;
(3)若该校八年级有学生1000人,请你算出喜爱英语的人数,并发表你的看法.