题目内容
 如图,已知AB=DE,BC=EF,AF=DC,则∠B=∠E,请说明理由(填空)
如图,已知AB=DE,BC=EF,AF=DC,则∠B=∠E,请说明理由(填空)解:AC=AF-CF,DF=DC-CF
∵AF=DC(已知)
∴AF-CF=DC-
在△ABC和△DEF中,
AC=DF
BC=
AB=
∴△ABC≌△DEF
∴∠B=∠E
考点:全等三角形的判定与性质
专题:证明题
分析:求出AC=DF,根据SSS推出△ABC≌△DEF,根据全等三角形的性质得出即可.
解答:解:∵AC=AF-CF,DF=DC-CF,AF=DC(已知)
∴AF-CF=DC-CF,
即AC=DF,
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS),
∴∠B=∠E(全等三角形的对应角相等),
故答案为:CF,EF,DE,已知,(SSS),(全等三角形的对应角相等).
∴AF-CF=DC-CF,
即AC=DF,
在△ABC和△DEF中,
|
∴△ABC≌△DEF(SSS),
∴∠B=∠E(全等三角形的对应角相等),
故答案为:CF,EF,DE,已知,(SSS),(全等三角形的对应角相等).
点评:本题考查了全等三角形的性质和判定的应用,主要考查学生的运用性质进行推理的能力,注意:全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
某机械厂一月份生产零件50万个,计划通过改革技术,使今后两月的产量都比前一月增长一个相同的百分数,使得三月份生产零件72万个.若设这个百分数为x,则可列方程为( )
| A、50(1+x)2=72 |
| B、50+50(1+x)2=72 |
| C、50(1+x)+50(1+x)2=72 |
| D、50+50(1+x)+50(1+x)2=72 |
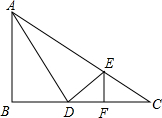 如图,在△ABC中,∠B=90°,AB=8,BC=16,D在边BC上,BD=6,AD⊥DE交AC于点E,EF⊥BC于点F.
如图,在△ABC中,∠B=90°,AB=8,BC=16,D在边BC上,BD=6,AD⊥DE交AC于点E,EF⊥BC于点F. 如图所示,点P是正方形ABCD内一点,且AB=5cm,BP=4cm,AP=3cm,现将△ABP绕点B旋转到△CBE,求PE的长.
如图所示,点P是正方形ABCD内一点,且AB=5cm,BP=4cm,AP=3cm,现将△ABP绕点B旋转到△CBE,求PE的长. 根据俯视图画出主视图和左视图.
根据俯视图画出主视图和左视图. 如图,已知反比例函数y=
如图,已知反比例函数y=