题目内容
3.利用图象解下列方程组.(1)$\left\{\begin{array}{l}{y=-x}\\{y=\frac{1}{2}x+\frac{3}{2}}\end{array}\right.$
(2)$\left\{\begin{array}{l}{x+y=-1}\\{x-y=2}\end{array}\right.$.
分析 (1)在同一平面直角坐标系中画出函数y=-x和y=$\frac{1}{2}$x+$\frac{3}{2}$的图象,两函数图象的交点就是方程组的解;
(2)首先把二元一次方程整理成一次函数得y=-x-1和y=x-2,然后在同一平面直角坐标系中画出它们的图象,两函数图象交点就是方程组的解.
解答 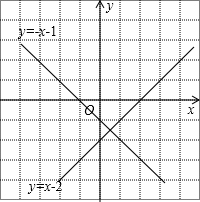
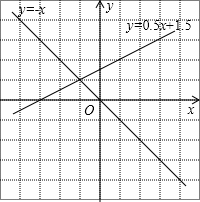 解:(1)如图所示:
解:(1)如图所示:
∵两函数图象交于点(-1,1),
∴方程组的解为$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$;
(2)如图所示:
∵两函数图象交点为($\frac{1}{2}$,-$\frac{3}{2}$),
∴方程组的解$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=-\frac{3}{2}}\end{array}\right.$.
点评 此题主要考查了一次函数与二元一次方程组的关系,关键是掌握两函数图象的交点就是方程组的解.

练习册系列答案
相关题目
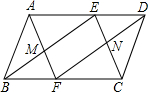 已知,如图,在平行四边形ABCD中,点E在AD上,连接BE,DF∥BE交BC于点F,AF与BE交于点M,CE与DF交于点N.求证:EF与MN互相平分.
已知,如图,在平行四边形ABCD中,点E在AD上,连接BE,DF∥BE交BC于点F,AF与BE交于点M,CE与DF交于点N.求证:EF与MN互相平分.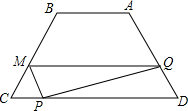 如图,等腰梯形ABCD中,AB=4,CD=9,∠C=60°,动点P从点C出发沿CD方向向点D运动,动点Q同时以相同的速度从点D出发沿DA方向向终点A运动,进点Q作QM∥CD交BC于点M,连接MP(其中一个动点到达端点时,另一个动点也随之停止运动).设CP=x
如图,等腰梯形ABCD中,AB=4,CD=9,∠C=60°,动点P从点C出发沿CD方向向点D运动,动点Q同时以相同的速度从点D出发沿DA方向向终点A运动,进点Q作QM∥CD交BC于点M,连接MP(其中一个动点到达端点时,另一个动点也随之停止运动).设CP=x