题目内容
9.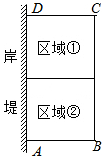 为了节省材料,某水产养殖户利用水库的岸堤为一边,用总长为a米(a为大于21的常数)的围网在水库中围成了如图所示的①②两块矩形区域.已知岸堤的可用长度不超过21米.设AB的长为x米,矩形区域ABCD的面积为y平方米
为了节省材料,某水产养殖户利用水库的岸堤为一边,用总长为a米(a为大于21的常数)的围网在水库中围成了如图所示的①②两块矩形区域.已知岸堤的可用长度不超过21米.设AB的长为x米,矩形区域ABCD的面积为y平方米(1)求y与x之间的函数关系,并直接写出自变量x的取值范围(用含a的式子表示).
(2)若a=30,求y的最大值,并求出此时x的值.
(3)若a=48,请求出y的最大值.
分析 (1)设AB的长为x米,则BC的长为(a-3x)米,根据矩形民机公式可得函数解析式,由0<BC≤21可得x的范围;
(2)将a=30代入解析式配方成顶点式,结合x的范围可得最值;
(3)将a=48代入解析式配方成顶点式,结合x的范围可得最值.
解答 解:(1)设AB的长为x米,则BC的长为(a-3x)米,
根据题意得:y=x(a-3x)=-3x2+ax,
由a-3x≤21可得x≥$\frac{a-21}{3}$,
由a-3x>0得x<$\frac{a}{3}$,
∴$\frac{a-21}{3}$≤x<$\frac{a}{3}$;
(2)当a=30时,y=-3x2+30x=-3(x-5)2+75,
∵3≤x<10,
∴当x=5时,y取得最大值为75;
(3)当a=48时,y=-3x2+48x=-3(x-8)2+192,
∴当x=8时,y取得最大值为192.
点评 本题主要考查二次函数的应用,根据矩形面积公式得出函数解析式,利用二次函数的顶点式,结合二次函数的性质得出其最值情况是解题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
19. 如图,是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
如图,是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
 如图,是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
如图,是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )| A. | 美 | B. | 丽 | C. | 港 | D. | 城 |
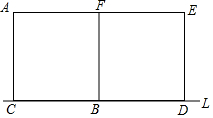 如图,已知边长等于8个单位长度的两个完全相同的正方形ACBF、BDEF有公共边BF,且CB与BD均在直线L上,将正方形ACBF沿直线L以1单位/秒向右平移,设移动时间为t秒,正方形ACBF在移动过程中与正方形BDEF重叠的面积为S,试求:
如图,已知边长等于8个单位长度的两个完全相同的正方形ACBF、BDEF有公共边BF,且CB与BD均在直线L上,将正方形ACBF沿直线L以1单位/秒向右平移,设移动时间为t秒,正方形ACBF在移动过程中与正方形BDEF重叠的面积为S,试求: